J Pharm Pharmaceut Sci (www.cspscanada.org) 10(3):263-277, 2007
Solubility prediction of drugs in water-cosolvent mixtures using Abraham solvation parameters
A. Jouyban1, Sh. Soltanpour2, S. Soltani3, H.K. Chan4, W.E. Acree5
1Faculty of Pharmacy and Drug Applied Research Center, Tabriz University of Medical Sciences, Tabriz, Iran; 2Kimia Research Institute, Tabriz; Iran; 3Biotechnology Research Center, Tabriz University of Medical Sciences, Tabriz, Iran; 4Faculty of Pharmacy, The University of Sydney, Sydney NSW 2006, Australia; 5Department of Chemistry, University of North Texas, Denton, TX, USA
Received January 27, 2007; Revised April 3, 2007; Accepted April 28, 2007; Published May 19, 2007.
Corresponding Author: Dr. A. Jouyban, Faculty of Pharmacy, Tabriz University of Medical Sciences, Tabriz 51664, Iran, Email: ajouyban@hotmail.com
ABSTRACT - PURPOSE. To provide predictive cosolvency models, the Abraham solvation parameters of solutes and the solvent coefficients were combined with the Jouyban-Acree and the log-linear models. These models require two and one solubility data points to predict the solubility of drugs in water-cosolvent mixtures. Ab initio prediction methods also were employed and the results were discussed. METHOD. The Jouyban-Acree model constants were correlated with variables derived from the Abraham solvation parameters of solutes and the solvent coefficients to present quantitative structure property relationship (QSPR) models. The calculated model constants using the QSPR models were used to predict the solubility in water-cosolvent mixtures. The mean percentage deviation (MPD), average absolute error (AAE) and root mean square error (RMSE) criteria were calculated to show the accuracy of the predictions. RESULTS. The overall MPD (±SD) of the proposed method employing solubility data in mono-solvents, i.e. two data points for each set, was 18.5±12.0 which indicates an acceptable prediction error from the practical point of view. The best cosolvency model employing aqueous solubility data was produced overall MPD of 75.2±72.6. The overall MPD of the proposed ab initio method was 74.9±19.3%. The models produced the same accuracy pattern considering MPD, AAE and RMSE criteria. CONCLUSION. The proposed model employing two solubility data points for each set produced acceptable prediction error (»18 %) and could be recommended for practical applications in pharmaceutical industry. MPD, AAE and RMSE criteria produced similar results considering various models. However, MPD criterion was preferred since its numerical values could be compared with experimental relative standard deviations for repeated experiments.
Introduction
Solubility of drugs in water-cosolvent mixtures could be mathematically represented using various models. These models cover from the pioneering and the simplest cosolvency model of Yalkowsky (1) to a relatively complex fluctuation model of Ruckenstein and Shulgin (2). Available cosolvency models have been reviewed and to address the diversity of the models, all models have been converted to a unified cosolvency model in a recent work (3). From these models, the log-linear equation of Yalkowsky has often been preferred, because of its simplicity and applicability in pharmaceutical industry where researchers are more interested in models requiring simple and easy computational operations.
Solubility prediction in water-cosolvent mixtures with an acceptable error range is one of the main goals of cosolvency modeling. The produced prediction errors for such models are relatively high and thus far, an accurate predictive model has not been proposed. Recently, trained versions of the Jouyban-Acree model has been presented for solubility prediction of drugs in water-dioxane (4), water-ethanol (5), water-propylene glycol (6) and water-polyethylene glycol 400 (7) mixtures. These prediction methods should be trained for each cosolvent and also require experimental solubility data of the drug in neat water and the cosolvent as input data. An ab initio prediction method (without using any experimentally determined data) for solubility of drugs in water-cosolvent mixtures is of great importance in drug discovery studies specially in the first stages which scarce amount of the drug/drug candidate is available and in some cases, the aqueous solubility is low and should be increased using solubilization techniques including cosolvency. The main task at this stage is to find a cosolvent suitable for dissolving the desired amount of the drug. The common method to address the task is the trial and error approach which is time consuming and costly. The aims of this work are to: 1) propose a general trained version of the Jouyban-Acree model for solubility prediction of drugs in water-cosolvent mixtures using solubility of the drug in mono-solvent systems, 2) represent prediction methods employing a single solubility datum using log-linear and Abraham models, 3) provide an ab initio solubility prediction method in water-cosolvent mixtures by using both the log-linear model of Yalkowsky with Abraham solvation model and 4) predict the optimum solvent composition of water-cosolvent mixtures dissolving the maximum amount of a drug using the proposed method. The applicability of the methods was checked using available solubility data of drugs in water-cosolvent mixtures expressed in mole/L, with known solubility in water, neat cosolvent, Abraham solvation parameters and also Abraham solvent coefficients.
COMPUTATIONAL METHODS
Solubility prediction using two solubility data points
The Jouyban-Acree model provided accurate solubility data in water-cosolvent mixtures and its model constants were computed for four commonly studied cosolvents (4-7). The Jouyban-Acree model is:
![]() (1)
(1)
where Sm is the solute’s solubility in water-cosolvent mixtures, fc and fw the volume fractions of cosolvent and water in the absence of the solute, Sc and Sw the solubilities in neat cosolvent and water, respectively, T is the absolute temperature (K) and Ji are the model constants. Table 1 listed the numerical values of J0, J1 and J2, the number of solubility data sets (NDS) used in the training process of the model and the references. The numerical values of J0-J2 represent the extent of solute-solvent interactions in the solution. In a recent work (8), the J0-J2 terms were correlated to Abraham solvation parameters of the solutes and the solvent coefficients of water to solvent process (9).
The applicability of the method has been evaluated using 194 solubility data sets of five different chemicals in non-aqueous binary solvents and the predictions were in good agreement with the experimental solubilities. The basic quantitative structure property relationship (QSPR) was:
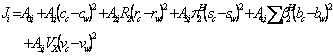 (2)
(2)
The term ![]() was omitted from the QSPR model, since
was omitted from the QSPR model, since ![]() of the studied chemicals were zero, however, the term could be added to equation 2 as:
of the studied chemicals were zero, however, the term could be added to equation 2 as:
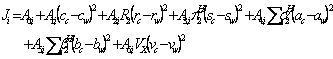 (3)
(3)
where A terms were the model constants (8), c, r, s, a, b and v are the solvents coefficients, subscripts c and w denote cosolvent and water, respectively, ![]() is the excess molar refraction,
is the excess molar refraction, ![]() is dipolarity/polarizability of the solute,
is dipolarity/polarizability of the solute, ![]() denotes the solute’s hydrogen-bond acidity,
denotes the solute’s hydrogen-bond acidity, ![]() stands for the solute’s hydrogen-bond basicity and
stands for the solute’s hydrogen-bond basicity and ![]() is the McGowan volume of the solute in unit of 0.01(cm3/mole). The Ji (i.e., J0, J1 and J2) terms of the studied solubility data sets were regressed against
is the McGowan volume of the solute in unit of 0.01(cm3/mole). The Ji (i.e., J0, J1 and J2) terms of the studied solubility data sets were regressed against ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() values to compute Aj,i terms, then the Aj,i terms were replaced in equation 1 and the solubility of drugs in binary solvents were predicted employing experimental values of Sc and Sw.
values to compute Aj,i terms, then the Aj,i terms were replaced in equation 1 and the solubility of drugs in binary solvents were predicted employing experimental values of Sc and Sw.
Table 1. Numerical values of the Jouyban-Acree model constants (J0, J1 and J2) for commonly studied cosolvents, the number of data sets (NDS) employed in the training process of the model and the references.
Cosolvent |
J0 |
J1 |
J2 |
NDS |
Reference |
Dioxane |
958.44 |
509.45 |
867.44 |
36 |
4 |
Ethanol |
724.21 |
485.17 |
194.41 |
26 |
5 |
Polyethylene glycol 400 |
394.82 |
-355.28 |
388.89 |
79 |
7 |
Propylene glycol |
37.03 |
319.49 |
- |
27 |
6 |
Solubility prediction using aqueous solubility datum
The algebraic mixing rule (1) or log-linear model was expressed by:
![]() (4)
(4)
and by replacing fw with (1-fc), equation 4 could be re-written as:
![]() (5)
(5)
The term ![]() was called cosolvency power (
was called cosolvency power (![]() ) and was correlated to the logarithm of octanol-water partition coefficient of the solutes (
) and was correlated to the logarithm of octanol-water partition coefficient of the solutes (![]() ) using:
) using: ![]() (6)
(6)
Where M and N are the model constants which are specific for the cosolvent and independent from the solute (10). The numerical values of M and N terms for the studied cosolvents are listed in Table 2. With known M and N terms along with Sw and ![]() values, one can predict solubility of a drug in water-cosolvent mixtures.
values, one can predict solubility of a drug in water-cosolvent mixtures.
The Abraham solvation parameter model provided a solubility prediction method for solutes dissolved in a wide variety of neat organic solvents (9, 11). The Abraham model employs five descriptors for each solute and six solvent coefficients that were computed for a number of common solvents (11). The basic model for processes within condensed phases is:
![]() (7)
(7)
The c, r, s, a, b and v (solvent’s coefficients), which depend upon the solvent system under consideration. Numerical values of the coefficients have been reported in the literature (11) for several water-to-organic solvent systems. Equation 7 could be written as:
![]() (8)
(8)
Table 2. Numerical values of M, N and number of data sets (NDS) employed in the training process of the model (data taken from a reference (10)).
Cosolvent |
M |
N |
NDS |
Acetonitrile |
1.16 |
-0.49 |
10 |
Dioxane |
1.08 |
0.40 |
23 |
Ethanol |
0.95 |
0.30 |
197 |
Methanol |
0.89 |
0.36 |
79 |
Table 3. Details of experimental solubility data of solutes in water-cosolvent mixtures at various temperatures (t, °C), the logarithm of solubilities in neat cosolvent and water, the number of data points in each set (NDP), and the references
No. |
Solute |
Cosolvent |
t (°C) |
logSc |
logSw |
NDP |
Reference |
1 |
Aminopyrine |
Ethanol |
25 |
0.18 |
-0.64 |
11 |
15 |
2 |
Amobarbital |
Ethanol |
25 |
-0.01 |
-2.61 |
41 |
16 |
3 |
Antipyrine |
Ethanol |
25 |
0.52 |
0.35 |
11 |
15 |
4 |
Barbital |
Ethanol |
25 |
-0.30 |
-1.40 |
41 |
16 |
5 |
Benzocaine |
Dioxane |
5 |
-0.21 |
-2.70 |
11 |
17 |
6 |
Benzocaine |
Dioxane |
10 |
0.06 |
-2.52 |
11 |
17 |
7 |
Benzocaine |
Dioxane |
15 |
0.20 |
-2.40 |
11 |
17 |
8 |
Benzocaine |
Dioxane |
20 |
0.28 |
-2.39 |
11 |
17 |
9 |
Benzocaine |
Dioxane |
25 |
0.46 |
-2.25 |
9 |
17 |
10 |
Benzocaine |
Dioxane |
30 |
0.52 |
-2.15 |
8 |
17 |
11 |
Benzocaine |
Dioxane |
35 |
0.58 |
-2.01 |
8 |
17 |
12 |
Benzocaine |
Dioxane |
40 |
0.66 |
-2.00 |
7 |
17 |
13 |
Caffeine |
Dioxane |
25 |
-0.89 |
-1.00 |
16 |
18 |
14 |
Diazepam |
Ethanol |
30 |
-0.91 |
-3.74 |
11 |
19 |
15 |
Furosemide |
Ethanol |
25 |
-1.37 |
-3.89 |
13 |
20 |
16 |
Meloxicam |
Ethanol |
25 |
-0.45 |
-1.92 |
8 |
21 |
17 |
Metharbital |
Ethanol |
25 |
-0.67 |
-2.00 |
41 |
16 |
18 |
Pentobarbital |
Ethanol |
25 |
0.04 |
-2.66 |
40 |
16 |
19 |
Phenobarbital |
Ethanol |
25 |
-0.29 |
-2.29 |
41 |
16 |
20 |
Phenytoin |
Ethanol |
25 |
-1.23 |
-4.09 |
11 |
22 |
21 |
Phenytoin |
Methanol |
25 |
-1.03 |
-4.09 |
11 |
22 |
22 |
Salicylic acid |
Dioxane |
10 |
0.41 |
-2.10 |
11 |
17 |
23 |
Salicylic acid |
Dioxane |
20 |
0.49 |
-1.96 |
11 |
17 |
24 |
Salicylic acid |
Dioxane |
25 |
0.57 |
-1.92 |
8 |
17 |
25 |
Salicylic acid |
Dioxane |
30 |
0.60 |
-1.82 |
8 |
17 |
26 |
Salicylic acid |
Dioxane |
35 |
0.64 |
-1.77 |
8 |
17 |
27 |
Salicylic acid |
Dioxane |
40 |
0.67 |
-1.70 |
8 |
17 |
28 |
Salicylic acid |
Ethanol |
25 |
0.32 |
-1.86 |
11 |
23 |
29 |
Theophylline |
Acetonitrile |
25 |
-2.09 |
-1.47 |
17 |
24 |
30 |
Theophylline |
Methanol |
25 |
-1.48 |
-1.47 |
13 |
24 |
Table 4. Details of solutes Abraham solvation parameters, melting point (MP) and logarithm of partition coefficient (logKow) of the solutes studied with their references
No.a |
R2 |
|
|
|
Vx |
Reference for solvation parameters |
mp (°C) |
|
Reference for |
1 |
1.780 |
1.780 |
0.000 |
1.370 |
1.870 |
25 |
108.0 |
0.90 |
26 |
2 |
1.030 |
1.110 |
0.470 |
1.230 |
1.797 |
27 |
157.0 |
2.07 |
26 |
3 |
1.530 |
1.580 |
0.000 |
1.050 |
1.480 |
25 |
111.5 |
0.23 |
14 |
4 |
1.030 |
1.140 |
0.470 |
1.180 |
1.374 |
27 |
189.0 |
0.65 |
26 |
5 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
6 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
7 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
8 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
9 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
10 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
11 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
12 |
1.034 |
1.040 |
0.320 |
0.820 |
1.313 |
27 |
89.0 |
1.97 |
28 |
13 |
1.940 |
1.810 |
0.000 |
1.470 |
1.360 |
25 |
238.0 |
-0.07 |
28 |
14 |
2.380 |
2.110 |
0.000 |
1.150 |
2.070 |
25 |
125.5 |
2.99 |
29 |
15 |
2.050 |
2.550 |
1.360 |
1.470 |
2.100 |
25 |
206.0 |
1.51 |
29 |
16 |
2.880 |
3.570 |
0.580 |
1.910 |
2.320 |
25 |
254.0 |
2.80 |
29 |
17 |
1.092 |
1.160 |
0.210 |
1.190 |
1.515 |
27 |
150.5 |
1.14 |
26 |
18 |
1.630 |
1.800 |
0.730 |
1.150 |
1.700 |
27 |
129.5 |
2.07 |
26 |
19 |
1.030 |
1.110 |
0.470 |
1.230 |
1.797 |
27 |
174.0 |
1.47 |
26 |
20 |
1.713 |
2.190 |
0.850 |
1.000 |
1.869 |
25 |
295.0 |
2.47 |
26 |
21 |
1.713 |
2.190 |
0.850 |
1.000 |
1.869 |
25 |
295.0 |
2.47 |
26 |
22 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
23 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
24 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
25 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
26 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
27 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
28 |
1.050 |
0.890 |
0.720 |
0.380 |
0.990 |
25 |
158.0 |
2.24 |
28 |
29 |
1.930 |
1.840 |
0.420 |
1.380 |
1.220 |
25 |
272.5 |
-0.02 |
26 |
30 |
1.930 |
1.840 |
0.420 |
1.380 |
1.220 |
25 |
272.5 |
-0.02 |
26 |
a Details of data sets are the same as Table 3.
Table 5. The coefficients of equation 7 taken from a reference (11)
Solvent |
c |
e |
s |
a |
b |
v |
|
|
|
|
|
|
|
Acetonitrile |
0.413 |
0.077 |
0.326 |
-1.566 |
-4.391 |
3.364 |
Dioxane |
0.098 |
0.350 |
-0.083 |
-0.556 |
-4.826 |
4.172 |
Ethanol |
0.208 |
0.409 |
-0.959 |
0.186 |
-3.645 |
3.928 |
Methanol |
0.329 |
0.299 |
-0.671 |
0.080 |
-3.389 |
3.512 |
Water |
-0.994 |
0.577 |
2.549 |
3.813 |
4.841 |
-0.869 |
By replacing right hand side of equation 8 with the parenthesis term of equation 5:
![]() (9)
(9)
and using equation 9, it is possible to predict solubility of solutes in water-cosolvent mixtures employing aqueous solubility of the drug.
Ab initio solubility prediction
Variuos equations were reported to predict aqueous solubility of drugs including the general solubility equation (GSE) of Yalkowsky and Valvani (12) and the amended solvation energy relationship (ASER) of Abraham and Le (13). The GSE and ASER are:
![]() (10)
(10)
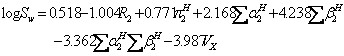 (11)
(11)
where mp is the melting point of the solute (°C). An updated version of ASER (UASER) was presented by Stovall et al. (11) as:
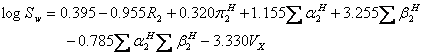 (12).
(12).
The log Sw term of equations 5 and 9 could be predicted using equations 7, 11 and/or 12, and it is possible to employ the models as an ab initio method. In addition, mean predicted solubility (MPS) of drugs in water is also checked for providing better predictions.
Accuracy criteria
The accuracies of the GSE and ASER have been compared (14) using the average absolute error (AAE) and the root mean square error (RMSE) criteria defined as:
![]()
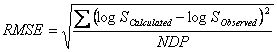
in which NDP is the number of solubility data points. Yang et al. (14) compared the GSE and ASER models employing aqueous solubility of 664 organic compounds and found that both models produced comparable accuracies. The AAE and RMSE of GSE were 0.45 and 0.62, respectively, and those of the UASER were 0.43 and 0.62. It has also been concluded that the mean predicted logSw provided better predictions as the AAE and RMSE of the mean predicted logSw were 0.38 and 0.53 (14).
The mean percentage deviation (MPD) is also used to check the accuracy of the prediction methods in this work and is calculated using:
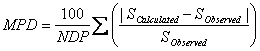
MPD values are comparable with experimental relative standard deviation (RSD) values for repeated experiments, therefore, we prefer to use MPD criterion. However, to compare the accuracy of the proposed method with the accuracies of GSE and ASER methods, AAE and RMSE criteria were also computed for predicted solubilities in this work.
RESULTS
Solubility prediction using two solubility data points
The 30 available data sets (15-24) of drug solubilities in mole/L unit (for details and the required parameters (11, 25-29) see Tables 3-5), were fitted to equation 1 for computing the numerical values of J0-J2 and then these constants were used to calculate the model constants of the proposed QSPR model (i.e. equation 3). The resulted QSPR models for predicting J0-J2 are as:
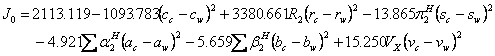 (13)
(13)
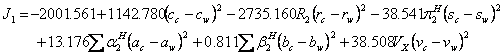 (14)
(14)
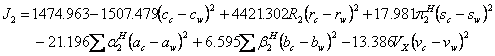 (15).
(15).
Using equations 13-15, J0-J2 could be easily predicted employing solute’s Abraham parameters and solvent coefficients. To check the accuracy of the proposed QSPRs for computing solubility data of drugs, the calculated J0-J2 constants for each data set along with the experimental solubility data of the drug in water and neat cosolvent were used to calculate the solubility in water-cosolvent mixtures and the results of MPDs were listed in Table 6. The best results (2.6 %) was found for metharbital in water-ethanol mixtures, the wrost one (66.2 %) was for antipyrine in water-ethanol mixtures and the overall MPD (±SD) was 18.5 (±12.0). The overall MPD (±SD) was reduced to 16.8 (±8.1) after excluding MPD of antipyrine (see column 2 of Table 6). Figure 1 showed the relative frequency of residuals for the models studied and the Jouyban-Acree model provided the best residual distribution as all residuals were in the range of -0.5 to 0.25.
As noted in Introduction, prediction of the solvent composition (fc,max) providing the maximum solubility (Sm, max) is crucial for preformulation studies. The proposed method is able to predict the volume fraction of the cosolvent to achieve the maximum solubility in a water-cosolvent mixture. Table 7 listed the experimentally observed and predicted fc, max using the Jouyban-Acree model.
Solubility prediction using aqueous solubility datum
In searching the pharmaceutical literature, different aqueous solubility and logP values were found for some solutes. The possible reasons for different aqueous solubilities could be: 1) solute purity; 2) insufficient equilibration time; 3) uncontrolled temperatures during solubility measurement; 4) analysis method employed; 5) laboratory techniques used; 6) typographical errors in reporting data; 7) polymorphism (30) and 8) enantiomeric forms of a solute (31). The impact of different Sw and logP values of the solutes on the solubility prediction in water-cosolvent mixtures is also studied by computing MPDs.
The commonly used single point solubility prediction method in water-cosolvent mixtures is the log-linear model of Yalkowsky (equation 5) in combination with the cosolvency power approach (equation 6). The minimum MPD (33.7 %) was observed for metharbital in water-ethanol mixtures and the maximum MPD (804.3 %) was for meloxicam in water-ethanol mixtures. The overall MPD of this numerical analysis after excluding MPD of meloxicam was 51.6 (± 8.6) % (see column 3 of Table 6).
Equation 9 produced the lowest MPD of 28.2 % for phenobarbital in water-ethanol mixtures, and the highest MPD of 451.2 % for antipyrine in water-ethanol mixtures. This data set produced reasonable results for other numerical methods including ab initio method and this observation means that there is an error in logSw of antipyrine. To confirm this assumption, various available logSw were used to predict the solubilities in water-ethanol mixtures; with logSw=0.7 (14) MPD was 1104.7, logSw=-0.6 (32) MPD was 69.2, logSw=-0.56 (25) MPD was 69.2 and logSw=0.48 (33) MPD was 627.4 %. To avoid any bias, the MPD of antipyrine (451.2 %) was excluded from computing overall MPD and the obtained MPD (±SD) was 62.2 (±15.2) % (see column 4 of Table 6).
Ab initio solubility prediction
Predicted aqueous solubility of drugs using GSE, ASER, UASER and their mean predicted solubilities (MPS) were used to compute the MPD values and listed in Table 8. Although GSE, ASER, UASER and MPS were developed to calculate aqueous solubility at 25 °C, there were no significant differences between the MPDs for all temperatures studied and those at 25 °C as shown in the last rows of Table 8. A possible reason for such an observation should be underestimated aqueous solubilities using the mentioned models.
Table 6. The number of required experimental data for various models, the mean precentage deviations (MPDs), overall MPD, standard deviations (SD) for all data sets and after exclusion of a data set producing the maximum MPD for each model
No.a |
Jouyban-Acree +Sc+Sw |
Cosolvency power + Sw |
Equation 9+ Sw |
Equation 9 + GSE |
Equation 9 + UASER |
Equation 9 + MPS |
1 |
21.8 |
40.0 |
93.8 |
64.5 |
97.7 |
87.0 |
2 |
12.4 |
57.1 |
58.1 |
76.4 |
80.3 |
58.1 |
3 |
66.2 |
60.6 |
451.2 |
69.2 |
98.0 |
88.1 |
4 |
6.7 |
42.9 |
51.8 |
80.0 |
78.4 |
45.2 |
5 |
23.2 |
64.0 |
78.7 |
82.3 |
144.5 |
114.5 |
6 |
17.5 |
60.3 |
76.6 |
80.2 |
113.6 |
100.7 |
7 |
13.2 |
59.2 |
76.6 |
74.0 |
92.0 |
85.2 |
8 |
12.1 |
64.3 |
79.3 |
77.6 |
86.8 |
83.1 |
9 |
5.1 |
58.3 |
74.5 |
73.2 |
81.1 |
77.9 |
10 |
7.8 |
52.7 |
71.1 |
70.1 |
72.1 |
70.1 |
11 |
15.5 |
44.8 |
67.3 |
67.2 |
66.8 |
65.8 |
12 |
9.5 |
48.1 |
68.8 |
68.5 |
67.2 |
67.3 |
13 |
19.3 |
54.2 |
82.1 |
95.1 |
74.7 |
69.3 |
14 |
23.4 |
47.2 |
47.1 |
72.8 |
83.4 |
52.3 |
15 |
31.7 |
53.9 |
53.8 |
660.6 |
459.4 |
68.5 |
16 |
14.7 |
804.3 |
73.6 |
99.9 |
97.4 |
99.4 |
17 |
2.6 |
33.7 |
44.1 |
38.9 |
120.1 |
95.0 |
18 |
28.4 |
68.5 |
77.2 |
76.4 |
72.4 |
76.2 |
19 |
15.0 |
51.9 |
28.2 |
46.5 |
35.7 |
36.6 |
20 |
20.6 |
52.8 |
52.1 |
87.3 |
279.5 |
51.8 |
21 |
35.3 |
43.8 |
41.3 |
84.3 |
367.2 |
44.6 |
22 |
25.3 |
50.7 |
62.4 |
97.2 |
52.3 |
68.7 |
23 |
17.8 |
52.6 |
61.6 |
97.4 |
51.8 |
74.9 |
24 |
13.9 |
48.2 |
57.2 |
97.0 |
49.5 |
73.4 |
25 |
14.4 |
49.0 |
54.0 |
97.1 |
51.0 |
76.2 |
26 |
15.2 |
51.2 |
54.4 |
97.1 |
54.2 |
78.4 |
27 |
16.3 |
54.9 |
54.1 |
97.2 |
60.7 |
80.8 |
28 |
25.9 |
35.7 |
35.8 |
94.4 |
43.4 |
51.3 |
29 |
3.8 |
57.3 |
70.0 |
90.2 |
270.4 |
99.0 |
30 |
19.8 |
37.9 |
58.9 |
86.6 |
380.8 |
106.6 |
|
|
|
|
|
|
|
Overall MPD |
18.5 |
76.7 |
75.2 |
100.0 |
122.8 |
74.9 |
SD |
12.0 |
137.7 |
72.6 |
106.9 |
110.5 |
19.3 |
|
|
|
|
|
|
|
Overall MPD after excluding a data set |
16.8 |
51.6 |
62.2 |
80.6 |
111.1 |
73.5 |
SD |
8.1 |
8.6 |
15.2 |
15.3 |
92.0 |
18.1 |
The predicted aqueous solubilities using GSE, ASER, UASER and MPS were employed to predict the solubility of drugs in water-cosolvent mixtures using equation 9. As noted above, using this method, no experimental solubility data is required to predict the solubility in water-cosolvent mixtures and the knowledge of melting point, logP and Abraham solvation parameters are required. The minimum and maximum MPD of predicted solubilities using equation 9 and GSE were 38.9 and 660.6 % respectively for metharbital and furosemide in water-ethanol mixtures (see column 5 of table 6). Different logKow values of furosemide were found in the literature and as it is expected, these values affected the predicted solubilities using GSE. Using logKow=2.6 (34) produced MPD was 53.3 % for furosemide. The overall MPD after excluding furosemide data was 81.5 (±15.4).
Predicted aqueous solubilities of drugs using ASER were used to predict the solubility of drugs in water-cosolvent mixtures and the MPD
range was 47.9-964.2 %. More details of this analysis were not reported in this work. The UASER and equation 9 was used to predict solubility in water-cosolvent mixtures and the minimum (35.7) and maximum (459.4) MPDs were observed for phenobarbital and meloxicam in water-ethanol mixtures. The overall MPD (±SD) after excluding the meloxicam MPD was 111.1 (± 92.0) % (see column 6 of Table 6).
As MPD values reported in Table 8 showed, the GSE, ASER and UASER models produced underestimated and/or overestimated aqueous solubilities, however, their mean values should be the closest solubilities to the experimental values and this fact was confirmed in our computations. Therefore, using MPS approach better predictions should be provided. The MPD range using MPS was 44.6 – 114.5 and the overall MPD (±SD) after excluding a data set with the highest MPD was 73.5 (±18.1) % (see the last column of Table 6).
Table 7. The experimental fc, max, the corresponding predicted values by the Jouyban-Acree model and differences between experimental and predicted values
No.a |
Experimental |
Predicted |
Difference |
|
|
|
|
1 |
0.70 |
0.80 |
-0.10 |
2 |
1.00 |
1.00 |
0.00 |
3 |
0.40 |
0.60 |
-0.20 |
4 |
0.85 |
0.85 |
0.00 |
5 |
0.90 |
0.80 |
0.10 |
6 |
0.90 |
0.90 |
0.00 |
7 |
0.90 |
0.90 |
0.00 |
8 |
0.90 |
0.90 |
0.00 |
9 |
0.90 |
0.90 |
0.00 |
10 |
0.90 |
0.90 |
0.00 |
11 |
0.90 |
0.90 |
0.00 |
12 |
0.90 |
0.90 |
0.00 |
13 |
0.40 |
0.65 |
-0.25 |
14 |
0.90 |
0.90 |
0.00 |
15 |
1.00 |
1.00 |
0.00 |
16 |
1.00 |
1.00 |
0.00 |
17 |
0.85 |
0.85 |
0.00 |
18 |
0.98 |
1.00 |
-0.03 |
19 |
0.90 |
0.85 |
0.05 |
20 |
0.90 |
1.00 |
-0.10 |
21 |
1.00 |
1.00 |
0.00 |
22 |
0.90 |
0.80 |
0.10 |
23 |
0.90 |
0.80 |
0.10 |
24 |
0.90 |
0.80 |
0.10 |
25 |
0.90 |
0.90 |
0.00 |
26 |
0.90 |
0.90 |
0.00 |
27 |
0.90 |
0.80 |
0.10 |
28 |
0.90 |
1.00 |
-0.10 |
29 |
0.23 |
0.23 |
0.00 |
30 |
0.46 |
0.46 |
0.00 |
a Details of data sets are the same as Table 3.
Table 8. The mean percentage deviation (MPD)a for predicted aqueous solubilities using various models
No. |
Solute |
t |
GSE |
ASER |
UASER |
MPS |
|
|
|
|
|
|
|
1 |
Aminopyrine |
25 |
74.1 |
87.5 |
98.6 |
92.4 |
2 |
Amobarbital |
25 |
47.9 |
-17.8 |
-204.1 |
-23.1 |
3 |
Antipyrine |
25 |
88.8 |
97.5 |
99.6 |
97.8 |
4 |
Barbital |
25 |
59.1 |
-176.9 |
-256.0 |
-59.2 |
5 |
Benzocaine |
5 |
-288.1 |
-974.7 |
-692.0 |
-591.3 |
6 |
Benzocaine |
10 |
-158.8 |
-616.5 |
-428.0 |
-360.9 |
7 |
Benzocaine |
15 |
-94.1 |
-437.3 |
-296.0 |
-245.6 |
8 |
Benzocaine |
20 |
-89.3 |
-424.2 |
-286.3 |
-237.2 |
9 |
Benzocaine |
25 |
-38.6 |
-283.8 |
-182.9 |
-146.9 |
10 |
Benzocaine |
30 |
-10.9 |
-207.1 |
-126.3 |
-97.5 |
11 |
Benzocaine |
35 |
20.0 |
-121.6 |
-63.3 |
-42.5 |
12 |
Benzocaine |
40 |
22.4 |
-114.9 |
-58.4 |
-38.3 |
13 |
Caffeine |
25 |
72.6 |
-5796.0 |
-137.0 |
-236.9 |
14 |
Diazepam |
30 |
-74.8 |
-29.9 |
75.7 |
18.0 |
15 |
Furosemide |
25 |
-1085.6 |
97.5 |
-771.9 |
-37.9 |
16 |
Meloxicam |
25 |
99.8 |
95.2 |
90.0 |
97.8 |
17 |
Metharbital |
25 |
-26.2 |
-753.0 |
-293.6 |
-248.6 |
18 |
Pentobarbital |
25 |
-9.8 |
39.6 |
-117.1 |
-13.0 |
19 |
Phenobarbital |
25 |
32.9 |
43.6 |
-45.7 |
18.0 |
20 |
Phenytoin |
25 |
73.4 |
-124.5 |
-692.6 |
-67.8 |
21 |
Phenytoin |
25 |
73.4 |
-124.5 |
-692.6 |
-67.8 |
22 |
Salicylic acid |
10 |
89.4 |
-255.9 |
-114.3 |
6.7 |
23 |
Salicylic acid |
20 |
92.3 |
-158.8 |
-55.8 |
32.2 |
24 |
Salicylic acid |
25 |
92.9 |
-137.3 |
-42.9 |
37.8 |
25 |
Salicylic acid |
30 |
94.3 |
-89.8 |
-14.3 |
50.3 |
26 |
Salicylic acid |
35 |
95.0 |
-67.5 |
-0.8 |
56.1 |
27 |
Salicylic acid |
40 |
95.7 |
-42.4 |
14.3 |
62.7 |
28 |
Salicylic acid |
25 |
93.8 |
-107.8 |
-25.1 |
45.5 |
29 |
Theophylline |
25 |
67.4 |
-2492.3 |
-1071.1 |
-362.7 |
30 |
Theophylline |
25 |
67.4 |
-2492.3 |
-1071.1 |
-362.7 |
|
|
|
|
|
|
|
|
MPD |
All data sets |
111.0 |
550.0 |
270.6 |
128.5 |
|
SD |
|
191.1 |
1168.0 |
312.0 |
140.7 |
|
|
|
|
|
|
|
|
MPD |
=25 |
123.8 |
762.8 |
346.6 |
118.6 |
|
SD |
=25 |
249.2 |
1518.8 |
362.2 |
114.5 |
Comparison of the models concerning various accuracy criteria
As noted under “Computational Methods”, MPD, AAE and RMSE criretia were used to express the accuracy of cosolvency models (4, 14). Figures 2-4 showed the overall MPD, AAE and RMSE and their standard deviations for various models. The accuracy order of the models considering MPD criterion was:
Jouyban-Acree model + Sc + Sw > Equation 9 + Sw ≈ Cosolvency power + Sw ≈ Equation 9 +MPS > Equation 9 + GSE > Equations 9 + UASER
After excluding a data set with the highest MPD, the accuracy order was the same. As a general rule, the more experimental data points employed by the model, the more accurate predictions provided.
Considering AAE criterion, the minimum and maximum AAEs, for Jouyban – Acree model were the same as those for MPDs, i.e. set numbers 17 and 3, respectively. As Figure 5 showed, there is high correlations between MPD, AAE and RMSE criteria. However, MPD criterion was preferred as it is comparable with RSD values for repeated experiments. The accuracy order considering overall AAE after excluding a data set for each model was:
Jouyban-Acree model + Sc + Sw > Cosolvency power + Sw > Equation 9 + Sw ≈ Equations 9 + UASER ≈ Equation 9 +MPS > Equation 9 + GSE.
A similar pattern was the case considering RMSE criterion. Figure 1 showed the relative frequency of residuals where the Jouyban-Acree model produced the best residual distribution and the most of other models produced underestimations.
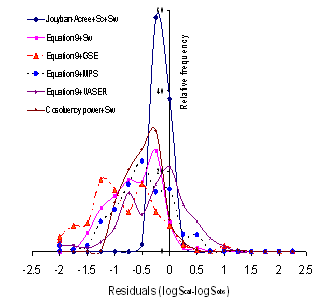
Figure 1. Relative frequency of residuals for models studied.
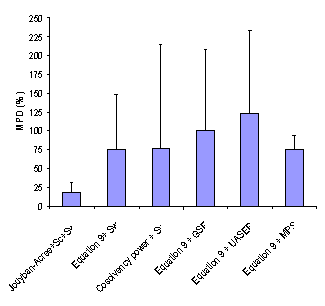
Figure 2. Overall mean percentage deviation (MPD (±SD)) for various numerical methods.
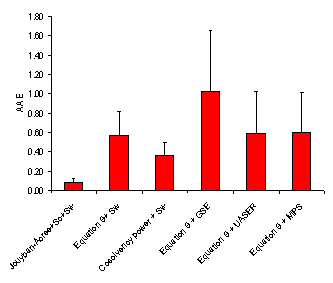
Figure 3. Overall average absolute error (AAE (±SD)) for various numerical methods
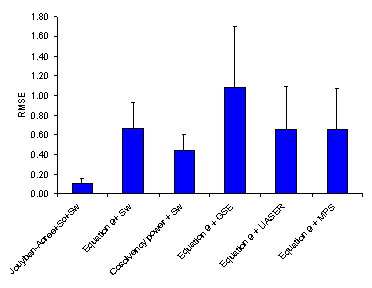
Figure 4. Overall root mean square error (RMSE (±SD)) for various numerical methods.
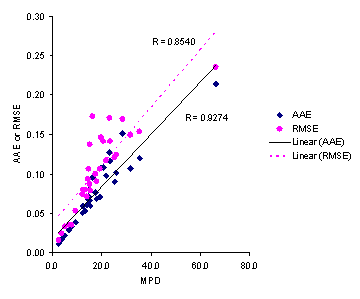
Figure 5. Correlations between AAE and RMSE with MPD accuracy criteria for solubilities predicted by the Jouyban-Acree model.
Discussion
Abraham solvation parameters were developed to calculate the properties of solutes including their solubility at 25 °C (9, 11). However, our observations reveal that using the combined Jouyban-Acree and Abraham models, it is possible to use the Abraham solvation parameters for calculating solubility at temperatures higher/lower than 25 °C. The main reason for such applicability is the employment of experimental Sw and Sc at the corresponding temperatures in the computations.
The proposed model provided reasonable fc, max predictions in comparison with the other numerical methods as in 57 % of the cases, the predicted fc, max was equal to the experimental value whereas the relative frequency for other models was 20 %. For some cases, there is no definite Sm, max value since the solubility profile in binary mixtures showed a plateau. As an example, there are no significant differences in logSm, max at fc=0.85 to 0.95, however, we have considered logSm, max= -0.24 and the corresponding fc (i.e. 0.90) as fc, max , where the predicted fc, max by the Jouyban-Acree model was 0.85, therefore, this case was not considered as a successful fc, max prediction in computations.
The Jouyban-Acree, equation 9 and cosolvency power approach of Yalkowsky (equations 5+6) provided more accurate predictions concerning the accuracy criteria. The main limitation of these models are their required experimental solubility data which are two data points for the Jouyban-Acree model and a single data point for the other models. The limitation could be overcomed by improvements in solubility prediction methods in mono-solvent systems.
CONCLUSION
A solubility estimation method for calculating drug solubility in water-cosolvent mixtures using ab initio method was provided by a combination of two well-established models. The expected prediction error is ~ 75% using MPS approach which is relatively high error when acceptable error range is considered. To provide better predictions, it was expected that including one experimental data point, i.e. Sw, reduces the prediction error. However, with slight reduction in the prediction errors, it is still relatively high and the expected error is ~ 60%. Employing two experimental data points improve the accuracy of the predictions within an acceptable error range and the expected error for this model (the Jouyban-Acree model) is ~ 18%. Therefore, collecting two data points and prediction of the solubility of drugs in water-cosolvent mixtures at temperatures of interest using the Jouyban-Acree model is recommended for industrial applications.
ACKNOWLEDGMENT
The financial support from the Drug Applied Research Center, Tabriz University of Medical Sciences (Grant No. 85-64) was gratefully acknowledged.