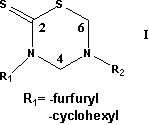
J Pharm Pharmaceut Sci (www.cspscanada.org) 8(3):586-592, 2005
Quantitative Structure Antitumoral-Activity Relationships of Thiadiazinthione Derivatives Using the Novel Hybrid Molecular Index pMRc
Ramón
Carrasco,a Juan A. Padrón,b
Rolando Pérez,c Hortensia Rodríguez,c Margarita Suárez,c
Carmen Ochoad
aDept. Química,
Centro de Química
Farmacéutica, La Habana, Cuba
bLaboratorio de Química Computacional y
Teórica, Facultad de Química, Universidad de La Habana
cLaboratorio de Síntesis Orgánica, Facultad
de Química, Universidad de La Habana
dInstituto de Química Médica (CSIC)
Madrid, España
Received October 26, 2005; Revised November 18, 2005, Accepted November 25, 2003, Published December 1, 2005
Corresponding
author: Ramon Carrasco-Velar,
Dept. Química, Centro
de Química Farmacéutica, Ave. 21 y Calle 200, Apdo. 16042, La
Abstract
Purpose.
The recently defined
molar-refractivity-partition index was
applied to a family of 1,3,5-
thiadiazin-2-thione derivatives in
order to establish quantitative
structure-antitumoral models. The goal
of this effort is to establish the
relationships between the structure
and biological response of these
compounds.
Method. After the splitting of
the sample in two sets, their indices
were correlated against the measured
biological activity. The combined use
of our index with others had been able
to describe not only the topologic but
also the
Introduction
3,5-disubstituted-tetrahydro-2H-1,3,5-thiadiazin-2-thione derivatives (I) have a wide spectrum of antimicrobial activity.[1] Several studies related to the antifungic, antiviral, antihelmintic, and tuberculostatic activity of these compounds have been extensively reported.[1-3] Previously, two series of 3,5-disubstituted thiadiazinthiones have been synthesized and assayed in vitro and in vivo in order to obtain new antiparasitic chemical substances for assessment as potential antiprotozoal agents.[2] In a recent work the antitumoral activity of these compounds have been reported against several tumoral cell lines and also some features of the degradation pathways of this heterocycle[3] were outlined. Up to now, experimental evidence strongly suggests that the thiadiazinthione ring acts as a prodrug. [1] In a protic medium, the heterocycle undergoes a ring opening to form different active metabolites, which are indeed responsible of the biological activity [1]. The use of topologic and topographical indexes is widely accepted for molecular modeling. Recently, we reported the hybrid molar-refractivity-partition index (pMRc)[4,5], based on Randic algorithm [6] and Ghose and Crippen partitioned molecular refractivity [7], that have the capability to portray London dispersive forces from a different perspective than the molecular refractivity. Then, the aim of this work is to test the index capability to relate structural features of this compound family with their antitumoral activity.
Theoretical Details
Molar
Refractivity
The molar refractivity is a constitutive-additive property calculated by the Lorenz-Lorentz formula:
![]() (1)
(1)
where M is the molecular weight, n
is the refraction index and r the density, and its value depends only of the wavelength of the
light used to measure the refraction index. For a radiation of infinite
wavelength, the molar refractivity represents the real volume of the molecules
and its polarizability. Then, the molar refractivity is
related, not only to the volume of the molecules but also to the
Table
1. General
formula and substituents of the thiadiazinthiones employed
|
|
|||
|
Sample # 1 |
Sample # 2 |
||
|
Compound |
R2 |
Compound |
R2 |
|
M1A |
(CH2)5COOH |
M2-A |
(CH2)5COOH |
|
M1BS |
CH(COOH)-CH2-COOH |
M2BS |
CH(COOH)-CH2-COOH |
|
M1C |
CH2-COOH |
M2-C |
CH2-COOH |
|
M1DS |
CH(CH2Ph)-COOH |
M2-DS |
CH(CH2Ph)-COOH |
|
M1DRS |
CH(CH2Ph)-COOH |
M2DRS |
CH(CH2Ph)-COOH |
|
M1ES |
CH[CH(CH3)2]-COOH |
M2FS |
CH[(CH2)2COOH]-COOH |
|
M1FS |
CH[(CH2)2COOH]-COOH |
M2-GS |
CH(CH3)2-COOH |
|
M1GS |
CH(CH3)2-COOH |
M2-H |
CH2-CONH-CH2-COOH |
|
M1H |
CH2-CONH-CH2-COOH |
M2-JS |
CH(CH2CONH2)-COOH |
|
M1IS |
CH[(CH2)2SCH3]-COOH |
M2-M |
CH2-CH2-COOH |
|
M1JS |
CH(CH2CONH2)-COOH |
M2-NS |
C[CH2-CH(CH3)2]-COOH |
|
M1JR |
CH(CH2CONH2)-COOH |
|
|
|
M1K |
C[(CH3)2]-COOH |
|
|
|
M1M |
CH2-CH2-COOH |
|
|
|
M1NS |
C[CH2-CH(CH3)2]-COOH |
|
|
|
M1O |
Furfuryl |
|
|
Table
2. Atomic
refractivity values reported by Ghose et. al.
|
Atom
type |
Atomic Refractivity
|
Atom
type |
Atomic Refractivity
|
|
Csp3 |
2.8158 |
N
(Ar) |
2.7662 |
|
Csp2 |
3.8278 |
NO2 |
3.5054 |
|
Csp |
3.8974 |
Ar-N=X |
3.8095 |
|
C
(Ar) |
3.5090 |
F |
1.0632 |
|
C=X |
3.0887 |
Cl |
5.6105 |
|
H |
0.9155 |
Br |
8.6782 |
|
-O- |
1.6351 |
I |
13.8741 |
|
=O |
1.7956 |
Ssp3 |
7.3190 |
|
O=N |
2.1407 |
Ssp2 |
9.1680 |
|
Nsp3 |
3.0100 |
R-SO-R |
6.0762 |
|
Nsp2,
Nsp |
3.2009 |
R-SO2-R |
5.3321 |
The atomic contribution to molecular refractivity
calculated by Ghose and Crippen method
Ghose and Crippen defined 110 atom types, [7] representing most commonly occurring atomic states of carbon, hydrogen, oxygen, nitrogen, halogens, and sulphur in organic molecules to split the molar refractivity. They stated that this classification partially differentiates the polarizing effects of heteroatoms and the effect of overlapping with non-hydrogen atoms, although they accepted that this classification might be weak in differentiating the conjugation effects. The authors stated that the classification may not completely cover all organic molecules, and that addition of atom types is always feasible. Further on, the 110 atom types were reduced to 22 (table 2). They assumed that the sum of the atomic values (ai) is the molecular value of the molar refractivity (eq. 2):
![]() (2)
(2)
Graph theory. The Randic-type graph theoretical invariant
Graph theory is a branch of mathematics related to topology and combinatorial problems.[18] Different authors have reported a large number of topological and topographical indices as well as its broad and successful applicability in QSAR and QSPR studies. However, the principal problems of the use of this approach are related to the physical meaning and the information redundancy among indices of similar definition, commonly expressed by high correlation values. [19] In this sense, Randic postulated [20] that any novel molecular descriptor 1) need to be simple, 2) add more insights to the problem, 3) or to solve a unexplained problem by alternative schemes, among others features. Randic molecular connectivity index for path of order p ( pc) is defined as [6]:
![]() (3)
(3)
It was modified by Kier and Hall[21,22] by defining subgraphs Gj tree type in the G graph containing edges. To each vertex i of graph G is associated a term di (for example di = vi). After this, to each subgraph Gi with vertices j1,..., jh+1 is calculated the F magnitude (Eq. 4)
![]() (4)
(4)
The numbers F(di1, dj(h+1)) are then added in all the subgraph Gi.. To include the multiple bonds and heteroatoms, Kier and Hall suggested the employ of di as,
![]() (5)
(5)
where Zi is the total number of electrons, Zvi is the number of valence electrons and hi is the hydrogen atoms number bonded to atom i. The connectivity indices obtained by this formula are known as valence indices [22] and represented by pcv. A more detailed explanation of the graph theory and calculation procedures can be found elsewhere.[23]
Molar refractivity partition index
pMRc
Molar refractivity partition index[6,7] (pMRc) use the Randic-type graph-theoretical invariant, and is defined as follow (Eq. 6),
![]() (6)
(6)
where the sum is all over adjacent vertices in the graph. dMR(vi) is the atomic refractivity value of the vi atom. The atomic refractivity values of bonded hydrogen to heavy atoms are also added to this term, to take into account their contribution in the graph.
Experimental part
Table 1 shows the compound sets. Reported antitumoral activity [3] is shown in tables 3 and 5. Biological activity is given as log IC50 against HeLa cells (logA). All structures were optimized to 0.01 convergence by the semiempirical method PM3 [9,10] implemented in MOPAC 6.0 program. [11-13]
In all the indexes employed the superscript p and c indicates path and cluster order, respectively. Randić (pc) and valence (pccV), based on the vertices connectivity matrix and pe Estrada indices, in the edge connectivity matrix [14] were used as topological descriptors. As topographic descriptors, the pW, pWq, pWqC and per Estrada indices [14] were employed. The W indices are based in the matrix of the vertices, weighted by the bond orders, the charge density and the charge density with spatial correction respectively. In the case of per, the connectivity matrix of the edges is weighted with the bond orders. The c, cV, W, Wq, WqC, e and er were calculated with the MODEST program [15]. Both the bond orders and the charge density were taken from the output of the semiempirical calculations.
pMRc index was included to portray the importance of the
The 27 compounds in the sample were divided in two, according the nature of R1 substituent. Forward stepwise multiple regression analysis was employed to establish the quantitative regression models, using the STATISTICA package. [17] A statistical outlier was defined as any compound that failed in three of the several criteria included in the program. In such case it was excluded from the sample and the analysis was restarted. Both models were cross-validated, reporting the Q2 value.
Results and Discussion
The mechanism of the antitumoral action of these compounds is not well established. It has been previously described that, in biological environment, the thiadiazinthione ring breaks to generate active metabolites.
Since only two different substituents in position 1 are represented in the series, it is possible to use an indicator (dummy) variable (taking values 1 or 0 for the presence or not of a given substituent) to described the whole set. However, we had preferred to treat the sample separately. Therefore the sample was divided in two: Sample #1 with R1=furfuryl and Sample #2 with R1=cyclohexyl.
Analysis of the sample set
#1
This sample set includes
sixteen N1-furfuryl derivatives. After the exclusion of the compound
M1JS as a statistical outlier (predicted value error > 55 %)
the regression analysis affords the equation 7:
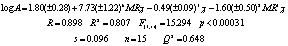 (7)
(7)
The prediction results
are shown in
table 3. According to Kubinyi,[18] the analysis for
the exclusion of statistical outliers must be an arbitrary process.
As the
exclusion of compound
M1DRS (error =
16.67%)
as a statistical outlier does not improve the quality of the model it was
maintained in the sample. Although
the
Q2 value of
the cross validation is higher than 0.5 (suggesting that the equation has
predictive capability), it is decreased by more than 10% with respect to the
R2 value of the regression
model. For this reason, we consider the predictive capability of the equation
as low, although Golbraigkh and Tropsha [19] accept
Q2 values higher than 0.5. The mean contribution to the
activity of each variable is 3.149, -3.314 and –0.666 for
6MRc,
3c and
2MR3c respectively. The analysis of these values suggests that the
inclusion of long fragments in the structure decreases the antitumoral
activity. This could be due to an increase in the possibility to form
instantaneous dipoles, taking into account the presence of heteroatoms as S and
O. Then, an increased macromolecular union described by this variable could
explain the role of the
The most important features that determine the antitumoral activity are the presence of fragments of three atoms and path-clusters combinations as described by variables 3c and 2MR3c respectively. Although it is risky to say that equation 7 is predictive, it was useful to evaluate which structural features are involved in the biological response of this compounds set in the HeLa assay.
The figures 1 and 2 show the plot of Predicted vs. Observed values and Residuals vs. Deleted Residuals from equation 7.
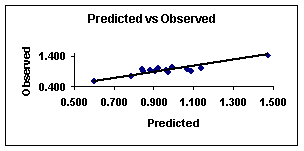
Figure
1.
Predicted vs. observed values for sample 1 with
equation 7
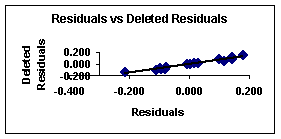
Figure
2.
Deleted vs. deleted residuals from equation 7
Summarizing, these results suggests that topological features and the dispersive forces described by the hybrid index pMRc affect the antitumoral activity of the compounds of sample 1, which can be associated to the presence of long fragments (up to six carbon atoms). These fragment types are also topologically described by the Randic index. The branching (2MR3c) and the size (6MRc, 3c) of the molecules in this sample may be the principal structural features that modulate the activity of these compounds.
The correlation matrix (table 4) demonstrates that correlation between variables in eq. 7 is less than 0.88, which is a good performance taking into account the nature of the variables employed in the analysis. [7]
If this equation is used only for classification as active or inactive, and the threshold of the error is accepted as 10 %, it can be concluded that 80% of the sample was correctly predicted.
Table
3.
Results, sample 1 with R1=
furfuryl
|
Compound |
R2 |
Exp. |
Pred. |
Res. |
% Error |
|
M1A |
(CH2)5COOH |
0.60 |
0.59 |
0.01 |
1.67 |
|
M1BS |
CH(COOH)-CH2-COOH |
0.96 |
0.97 |
-0.01 |
1.04 |
|
M1C |
CH2-COOH |
0.99 |
1.05 |
-0.06 |
6.06 |
|
M1DS |
CH(CH2Ph)-COOH |
1.06 |
0.98 |
0.09 |
8.49 |
|
M1DRS |
CH(CH2Ph)-COOH |
0.84 |
0.98 |
-0.14 |
16.67 |
|
M1ES |
CH[CH(CH3)2]-COOH |
0.90 |
0.90 |
0.00 |
0.00 |
|
M1FS |
CH[(CH2)2COOH]-COOH |
1.47 |
1.43 |
0.04 |
2.72 |
|
M1GS |
CH(CH3)2-COOH |
0.97 |
0.88 |
0.09 |
9.28 |
|
M1H |
CH2-CONH-CH2-COOH |
0.79 |
0.77 |
0.01 |
1.27 |
|
M1IS |
CH[(CH2)2SCH3]-COOH |
0.88 |
0.96 |
-0.08 |
9.09 |
|
M1JS |
CH(CH2CONH2)-COOH |
0.53 |
Outlier
|
||
|
M1JR |
CH(CH2CONH2)-COOH |
0.88 |
0.96 |
-0.08 |
9.09 |
|
M1K |
C[(CH3)2]-COOH |
0.92 |
1.02 |
-0.10 |
10.87 |
|
M1M |
CH2-CH2-COOH |
0.85 |
0.90 |
-0.06 |
7.06 |
|
M1NS |
C[CH2-CH(CH3)2]-COOH |
1.09 |
0.93 |
0.15 |
13.76 |
|
M1O |
Furfuryl |
1.13 |
1.02 |
0.11 |
9.73 |
|
Mean |
|
|
|
|
7.12 |
Table
4.
Correlation
matrix of variables in eq. 7.
|
|
Log A |
3c |
6MRc |
2MR3c |
|
Log A |
1.000 |
|
|
|
|
3c |
-0.237 |
1.000 |
|
|
|
6MRc |
-0.361 |
0.865 |
1.000 |
|
|
2MR3c |
-0.321 |
0.668 |
0.875 |
1.000 |
Analysis
of the sample set #2
This sample set includes the 11 derivatives where R1 = cyclohexyl. The regression analysis allows us to obtain the equation 8, which includes 1cv3 and 3MR3c indices. Both of them describe the role of molecular branching, but with different sign and fragments. The mean contribution values of each variable to the activity are -2.779 and 0.682 respectively.
This result suggests that
in this compound set topological features given by variable 1cv3
are more important than dispersive forces.
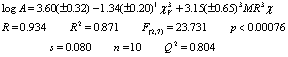 (8)
(8)
Activity prediction for sample 2 is shown in table 5.
Table
5.
Results, sample 2 with
R1= cyclohexyl
|
Compound |
R2 |
Exp. |
Pred. |
Res. |
% Error |
|
M2-A |
(CH2)5COOH |
1.48 |
1.42 |
0.06 |
4.05 |
|
M2BS |
CH(COOH)-CH2-COOH |
1.66 |
1.64 |
0.01 |
0.60 |
|
M2-C |
CH2-COOH |
1.46 |
1.55 |
-0.08 |
5.48 |
|
M2-DS |
CH(CH2Ph)-COOH |
1.14 |
1.29 |
-0.16 |
14.04 |
|
M2DRS |
CH(CH2Ph)-COOH |
1.37 |
1.29 |
0.08 |
5.84 |
|
M2FS |
CH[(CH2)2COOH]-COOH |
1.46 |
1.42 |
0.04 |
2.74 |
|
M2-GS |
CH(CH3)2-COOH |
1.14 |
1.14 |
0.00 |
0.00 |
|
M2-H |
CH2-CONH-CH2-COOH |
1.66 |
1.64 |
0.02 |
1.20 |
|
M2-JS |
CH(CH2CONH2)-COOH |
1.18 |
Outlier |
||
|
M2-M |
CH2-CH2-COOH |
1.54 |
1.54 |
0.00 |
0.00 |
|
M2-NS |
C[CH2-CH(CH3)2]-COOH |
1.18 |
1.16 |
0.02 |
1.69 |
|
Mean |
|
|
|
|
3.24 |
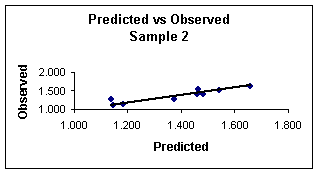
Figure 3.
Predicted
vs. observed values calculated with equation 8 for sample 2.
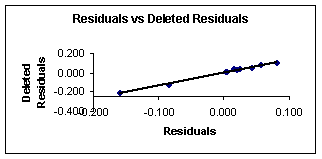
Figure 4. Residuals vs. deleted
residuals obtained from equation 8.
Figures 3 and 4 show the plots of the predicted vs. observed values with equation 8, and the graph of residuals vs. deleted residuals.
This last graph (fig. 4) suggests that this regression model is more stable than that given with equation 7 for the first compounds set. This can be explained from the definition of deleted residuals. They are the residuals that one would obtain if the respective case would be excluded from the estimation of the multiple regression (i.e., the computation of the regression coefficients).
Thus, if there are large discrepancies between the deleted residuals and the regular standardized residuals, then it can be concluded that the regression coefficients are not very stable, that is, they are greatly affected by the exclusion of single cases. If these results are analyzed in the same manner as for sample 1, it may be concluded that, qualitatively speaking, 90% of the sample was correctly predicted.
Conclusion
As a general remark, when the substituent in R1 is furfuryl, an increased activity is obtained except when R is CH[(CH2)2COOH]-COOH. Equations 7 and 8 suggest that the presence of path-cluster fragments type (2MR3c and 3MR3c respectively) in both series also increases the activity. These two features suggest that this pattern of substitution affords leads compounds in both series. On the other hand, it was determined that the pMRc index is useful to describe the antitumoral activity of the thiadiazinthiones set studied in this work. The index was able to discriminate between pure topological features and those related to dispersive forces.
Acknowledgements
This work has been partially supported by Ministry of Public Health of Cuba grants. The authors wish to thanks the referees and the editorial board for their useful comments and kindly patient.
References
[1] Ertan, M.; Bilgil, A.A.; Palaska, E. and
Yulug, N.; Synthesis and Antifungal Activities of some 3-(2-Phenylethyl)-5-substituted-tetrahydro-2-1,3,5-thiadiazine-2-thione,
Arzneimitttel Forschung-Drug Research,
42:160-171, 1992.
[2] a) Ochoa, C.; Pérez, E.; Pérez, R.;
Suárez, M.; Ochoa, E.; Rodríguez, H.; Barrio, A.G.; Muelas, S.; Nogal, J.J. and
Martínez, R.A.; Synthesis and Antiprotozoan Properties of New 3,5-Disubstituted-Tetrahydro-2H-1,3,5-Thiadiazin-2-Thione
Derivatives. Arzneimitttel Forschung-Drug
Research, 49:(II), 464-469, 1999. b) Muelas, S.;
Suárez, M.; Pérez, R.; Rodríguez, H.; Ochoa, C.; Escario, J.A. and Gómez-Barrio, A.; In Vitro and In Vivo Assays of 3,5-Disubstituted Tetrahydro-2H-1,3,5-thiadiazin-2-thione Derivatives
Against Trypanosoma cruzi. Mem. Inst.
Oswaldo Cruz, Río de Janeiro, 97:(2), 269-272, 2002.
[3] Pérez, R.; Rodríguez,
H.; Pérez, E.; Suárez, M.; Reyes, O.; González, L.J.; López de Cerain, A.; Ezpeleta, O.; Pérez, C. and Ochoa. C.; Study on the Decomposition Products of
Thiadiazinthione and their Anti-Cancer Properties. Arzneim. Forsch. -Drug Res.; 50(II): 854-857,
2000.
[4] Padrón, J.A.; Carrasco, R. and Pellón,
R.; Definition of New Descriptor Based on Molar Refractivity Partition Using
Randic Type Graph-Theoretical Invariant.; Revista Cubana de Farmacia, 34 Special Supp. Especial June
2000 pp. 328-2.
[5] Padrón, J. A.; Carrasco, R. and Pellón,
R.F.; Molecular Descriptor Based on a Molar Refractivity Partition using
Randic-type Graph-theoretical Invariant,
J.Pharm.Pharmaceut. Sci.(www.ualberta.ca/~csps)
5(3):234-231, 2002.
[6] Randic, M.; On Characterization of
Molecular Branching, J. Am. Chem. Soc.,
97:6609-6615, 1975.
[7] a) Ghose, A.K.
and Crippen, G.M.; Atomic Physicochemical Parameters for Three-dimensional
Structure-Directed Quantitative Structure-Activity Relationships. I. Partition
Coefficients as a Measure of Hydrophobicity. J.Comput.
Chem., 7:(4), 565-577, 1986; b) Ghose, A.K. and
Crippen, G.M.; Atomic Physicochemical Parameters for Three-Dimensional
Structure-Directed Quantitative Structure-Activity Relationships. 2. Modeling Dispersive and Hydrophobic Interactions; J. Comput. Chem.; 27(1):21-35, 1987.
[8] HyperChem,
(1993) Hypercube, Inc. and Autodesk, Inc. Release 3 for Windows.
[9] Stewart, J.J.P.; Optimization of
Parameters for Semi-empirical Methods I-Method; J.Comp.Chem., 10:209-220, 1989.
[10] Stewart, J.J.P.; Optimization of Parameters
for Semi-empirical Methods II-Applications;
J.Am.Chem.Soc. 10:221-264, 1989.
[11] Stewart, J. J. P.; MOPAC 6.0.
[12] Stewart, J. J. P.; Mopac: A
Semiempirical Molecular Orbital Program, J. Comp. Aid.
Mol. Design, 4(1): 1-103, 1990.
[13] MOPAC
v.6 for 3/486/Pentium PC’s. Release 1.02; March 1997; Windows 95 and NT
environments. Universidad de La Habana, Cuba, 1994-97.
[14] a) Estrada, E. and Montero,
[15] Rodríguez, L.; Estrada,
E.; Muñoz, I. and Gutiérrez Y.; MODEST (Molecular DESign Tools) 2.0.
Universidad Central de Las Villas: Santa Clara, 1994.
[16] Padrón, J.A. and Carrasco, R.; La Habana,
Program for the calculation of pMRc Index.
[17] STATISTICA
for WINDOWS, version 4.0, Statsoft, Inc. 1993.
[18] Harary,
F.; Graph Theory, Addison-Wesley,
[19]
[20] Kubinyi, H., QSAR: Hansch Analysis and
Related Approaches, pp. 59-60. In: Methods and Principles in Medicinal
Chemistry, R. Mannhold, P. Krogsgaard-Larsen y H. Timmerman, Eds. 1993,
[19] Golbraikh, A. and Tropsha, A. J. Mol. Graph. Model., 20, 269-276(2002).
[20] Randic, M.; Hansen, P.J. and Jurs, P.C.;
Search for Useful Graph Theoretical Invariants of Molecular Structure, J. Chem. Inf. Comput.Sci., 28:60-68,
1988.
[21] Kier, L.B. and Hall,
L.H.; Molecular Connectivity in Chemistry
and Drugs Research, Academic Press,
[22] Kier, L.B. and Hall,
L.H.; Molecular Connectivity in
Structure-Activity Analysis; Research Studies Press Ltd.,
[23] Molconn-Z 3.50 Manual; http://www.eslc.vabiotech.com/molconn/manuals/350/
Published by the Canadian Society for Pharmaceutical Sciences.
Copyright © 1998 by the Canadian Society for Pharmaceutical Sciences.