J Pharm Pharmaceut Sci (www.cspscanada.org) 9(1):113-118, 2006
Interdependency of pharmacokinetic parameters: A chicken-and-egg problem? Not!
Reza Mehvar
School of Pharmacy, Texas Tech University Health Sciences Center, Amarillo, Texas, USA
Received 24 February 2006, Accepted 27 February 2006, Published 09 March 2006
Corresponding Author: Reza Mehvar, Ph.D., School of Pharmacy, Texas Tech University Health Sciences Center, 1300 Coulter, Amarillo, TX 79106. reza.mehvar@ttuhsc.edu.
Abstract Pharmacokinetic (PK) software packages are widely used by scientists in different disciplines to estimate PK parameters. However, their use without a clear understanding of physiological parameters affecting the PK parameters and how different PK parameters are related to each other may result in erroneous interpretation of data. Often, mathematical relationships used for the estimation of PK parameters obscure the true physiological relationships among these parameters, prompting a discussion of which parameter came first and giving the appearance of the-chicken-and-the-egg dilemma. In this article, the author attempts to show how different PK parameters are related to physiological parameters and each other by using various scenarios and examples. In particular, the relationship between clearance and the rate of elimination and that among the other major PK parameters are explored. It is concluded that there is no dilemma in interdependency of the PK parameters, and the relationships among the PK parameters and between PK and physiological parameters are clear.
Introduction
The origin of pharmacokinetics is attributed to an article written by Torsten Torell in 1937 (1). After an initial fascination with mathematical relationships defining this discipline, came the introduction of a large number of easy-to-use pharmacokinetic (PK) software packages. Because of widespread application of pharmacokinetics in other disciplines, such as biology, pharmacology, and physiology, and the availability of software, the use of pharmacokinetics in biological sciences has grown substantially in the last two decades. However, the use of the PK software without a clear understanding of physiological parameters affecting the PK parameters and how different PK parameters are related to each other may result in erroneous interpretation of data.
One of the most common errors made by biological scientists, whose main focus and education are not in the area of pharmacokinetics, is the distinction between mathematical and physiological relationships among PK parameters (2). In other words, when two PK parameters are changed, which parameter is the cause and which one is the effect. For example, a recent heated discussion was erupted among some of the subscribers to the PharmPK LISTSERV†about whether the clearance of a drug is dependent on the rate of elimination or vice versa, with apparently no final resolution. The advocates of the dependency of CL on the rate of elimination (dAe/dt) cited the following equation as evidence:
![]() (1)
(1)
The argument is that because in practice, CL is sometimes determined from the rate of elimination, it is obvious that the latter influences the former. The proponents of the dependency of the rate of elimination to CL, on the other hand, state that the correct physiological presentation of the above equation is:
![]() (2)
(2)
with a definition of CL as the proportionality constant relating the rate of elimination to the blood concentration. This group argues that although in practice CL may be estimated using Equation 1, it is the rate of elimination that is dependent on CL, not vice versa.
This may seem a matter of semantics or give the impression of the-chicken-and-the egg dilemma. However, neither is true because there is indeed a clear physiologic cause and effect relationships among PK parameters, including clearance and rate of elimination, as demonstrated in the following sections.
It should be noted that the concepts presented here are not new and have been known by pharmacokineticists for many years. However, the aim of this presentation is to highlight the interdependence of PK parameters in an integrated and focused manner with some examples.
The
Relationship Between Clearance and Rate of Elimination
For illustration purposes, we shall select a hypothetical drug with elimination through hepatic metabolism only, although the same principles are valid for drugs with exclusive renal elimination or a combination of renal and hepatic elimination. Figure 1 demonstrates the cellular events in the liver that lead to the metabolism of drugs.
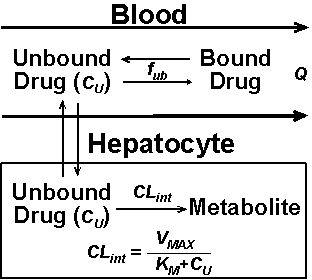
Figure 1:
Factors affecting the metabolism of a hypothetical drug by the liver enzymes.
The intrinsic capability of the liver enzymes in the hepatocytes to metabolize the drug (CLint) is dependent on the Michaelis-Menten constants, VMAX (maximum rate of metabolism) and KM (drug concentration producing half of VMAX), and drug concentration at the site of metabolism (Cu) as defined by the following equation:
![]() (3)
(3)
For majority of drugs, therapeutic concentrations result in Cu values much lower than KM, hence for these drugs CLint becomes a constant independent of the blood concentrations within the therapeutic range:
![]() (4)
(4)
This is not true for drugs such as phenytoin where therapeutic concentrations are close to the KM values. For these drugs, CLint decreases with an increase in the blood concentrations. For simplicity, we shall assume that our drug is metabolized by a single enzyme with a VMAX of 1.5 mg/min and a KM of 0.1 mg/L. Further, its therapeutic concentration ranges from 1 to 10 µg/L and its free fraction in blood (fub) is 0.1. This means that at therapeutic concentrations, the free drug concentrations (Cu) (0.1-1 µg/L) are much lower than KM (0.1 mg/L). Therefore, linear metabolism is expected within this range as CLint stays close to 15 L/min:
![]() (5)
(5)
It should be noted that this parameter (CLint) is the intrinsic capability of the liver to remove the drug in the absence of any supply (liver blood flow) limitation. However, as demonstrated in Fig. 1, the access of the liver enzymes to the drug is limited by other parameters such as the liver blood flow (Q), free fraction of the drug in the blood (fub), and permeability of the hepatocytes to the drug. However, in most cases, permeability of the hepatocytes to the drug is not the rate-limiting step in the metabolism of most drugs.
In the following sections, we will look at the metabolism of this hypothetical drug at a macro level by presenting three different scenarios.
Scenario 1: the basics
The metabolism of our hypothetical drug during one pass through the liver is depicted in Fig. 2.
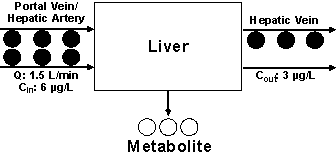
Figure 2: The
metabolism of a hypothetical drug in one single pass through the liver based on
Scenario 1 (see text for details).
For demonstration purposes, we assume that the concentrations of the drug entering and leaving the liver are 6 and 3 µg/L, respectively. This indicates that 50% of the drug entering the liver is converted to a metabolite or, in other words, the fraction of the drug extracted by one single-pass through the liver (extraction ratio, E) is 0.5. As demonstrated in Fig. 1, assuming high permeability, the extraction ratio (E) is dependent on Q, fub, and CLint. Several models have been proposed to define the relationship between E and its three determinants. One of the widely-used models is the well-stirred or venous equilibrium model, which defines this relationship using the following equation (3):
![]() (6)
(6)
Considering that the blood leaving the liver contains a concentration half of that entering the liver (Cin) (Fig. 2), one may state that half of the blood is totally cleared of the drug and the other half has the same concentration as Cin. In other words, half of the blood is cleared of the drug per unit of time. This is one of the definitions of clearance, which in this case is equivalent to 0.75 L/min (0.5 x 1.5 L/min), forming the basis of the following equation:
![]() (7)
(7)
Equations 6 and 7 clearly indicate both E and CL are dependent on fub, CLint, and Q. Substituting Equation 4 and 6 into 7 would clearly show the determinants of CL for a drug with linear metabolism:
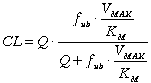 (8)
(8)
Any change in Q, fub, VMAX, and/or KM may potentially affect the CL of the drug. The degree of dependency of CL on any of these parameters, however, is influenced by the initial values of these parameters relative to each other, and its discussion is outside the scope of this communication.
Now that we have dealt with CL, let us consider the rate of elimination in our example (Fig. 2). Considering a Q of 1.5 L/min and the inlet and outlet concentrations of 6 and 3 µg/L, respectively, this means that the rate of elimination (metabolism) of the drug is 4.5 µg/min (1.5 L/min x 3 µg/L). The same value may also be obtained using Equation 2:
![]()
Scenario 2: a change in the blood concentration
Let us assume that the drug concentration entering the liver is now changed from 6 µg/L to 4 µg/L (Fig. 3). Because of the linear metabolism of the drug, the change in Cin is not expected to affect CLint, Q, or fub of the drug. Therefore, as Equation 6 suggests, the E of the drug (0.5) does not change. Consequently, the outlet concentration will be 2 µg/L in this case (Fig. 3). The CL of the drug, defined as the volume of blood cleared of drug per unit of time, also remains the same as that in Scenario 1 (0.75 L/min, Fig. 3). This is also consistent with the calculation of CL based on Equation 7 or 8, as none of the determinants of CL were changed. However, the rate of elimination of the drug in this case (1.5 L/min x 2 µg/L or 3 µg/min) will be lower than that in Scenario 1 (1.5 L/min x 3 µg/L or 4.5 µg/min). Again, the rate of elimination may also be estimated using Equation 2:
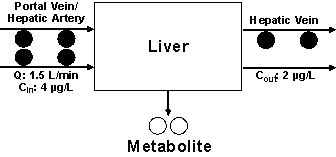
Figure 3: The metabolism of a hypothetical drug in one single pass through the liver based on Scenario 2 (a decrease in the inlet drug concentration; see text for details).
![]()
This observation indicates that the rate of elimination is dependent on the blood concentration of the drug, whereas CL is independent of blood concentration for a drug with linear pharmacokinetics.
Scenario 3: a change in the clearance
For this scenario, we shall change the CL of the drug and keep the inlet concentration the same as that in Scenario 1. Based on Equation 7, CL is dependent on Q and E. Additionally, E is dependent on Q, fub, and CLint (Equation 6), with the latter being dependent on VMAX and KM (Equation 4). A change in any of the determinants of CL, which are Q, fub, VMAX and KM (Equation 8), can potentially alter CL. Let us assume that the VMAX of the drug is increased by a factor of 2 from 1.5 mg/min to 3 mg/min as a result of an interacting drug. This in turn results in a two-fold increase in CLint from 15 L/min to 30 L/min:
![]()
The increased CLint will cause an increase in E and CL as demonstrated in Figure 4 and by Equations 6 and 7:
![]()
![]()
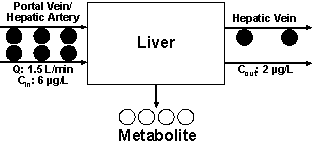
Figure 4: The
metabolism of a hypothetical drug in one single pass through the liver based on
Scenario 3 (an increase in the clearance; see text for details).
Figure 4 also clearly shows that the rate of elimination of the drug in this case is 6 µg/min (1.5 L/min x 4 µg/mL). As in the previous scenarios, the rate of elimination can also be calculated using Equation 2:
![]()
This scenario shows that when CL is changed, the rate of elimination of the drug changes proportionally.
Summary of scenarios
The three scenarios discussed above for a drug with linear pharmacokinetics suggest the following conclusions:
1. When the blood concentration of the drug changes, CL remains unchanged, whereas the rate of elimination of the drug changes proportionally. In other words, the change in the rate of elimination does not affect CL (Scenario 2). This shows the dependency of the rate of elimination to the blood concentration. Further, it shows the independence of CL from the rate of elimination.
2. When the blood concentration is kept constant and one of the determinants of CL is changed, the change in CL is proportionally reflected in a change in the rate of elimination, indicating the dependency of the rate of elimination on the CL and its determinants (Scenario 3).
3. Consequently, the rate of elimination is dependent on both the CL and blood concentration of the drug. Although CL is not affected by the rate of elimination, it is dependent on its determinants CLint, fub, and Q.
Coming back to the-chicken-and-the-egg dilemma, it is clear that there is no dilemma regarding the rate of elimination and CL; it is the rate of elimination that is dependent on CL and not vice versa. Therefore, although both Equations 1 and 2 are mathematically correct, only Equation 2 is physiologically valid. Researchers often use Equation 1 to estimate CL. However, it should not be forgotten that it is CL that determines the rate of elimination.
The
Relationships Among Other Pharmacokinetic Parameters
As the above discussion suggests, CL is a major PK parameter that is related to the efficiency of the eliminating organs, such as the liver and kidneys, to remove the drug from the body. Another major PK parameter, which is at the same level of importance as CL, is the volume of distribution (V), which is an indication of the extent of the distribution of the drug within the body. Similar to CL, V is determined by the physiological parameters of the patient and the physicochemical characteristics of the drug. The volume of distribution of drugs at steady state (VSS) is dependent on the volumes of blood (VB) and tissue (VT) and free fractions of the drug in blood (fub) and tissues (fut) according to the following equation (6):
![]() (9)
(9)
Both V and CL are independent parameters, meaning that a change in one does not necessarily result in a change in the other parameter, although there may be situations when a change in an underlying physiologic factor would affect both parameters (such as a change in fub).
A third major PK parameter is the elimination half life (t1/2) or rate constant (k). However, it should be noted that, in contrast to CL and V, t1/2 or k does not represent any single physiological process. Instead, it is a composite parameter, reflecting both CL and V processes 2). Therefore, although these three major parameters are mathematically related to each other, one should be aware that t1/2 or k is dependent on both CL and V and not vice versa. Therefore, although one may use the mathematical relationship presented in Equation 10 to estimate CL, one should be aware that the proper equations describing the interdependency of these three parameters are presented by Equations 11 and 12:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Conclusions
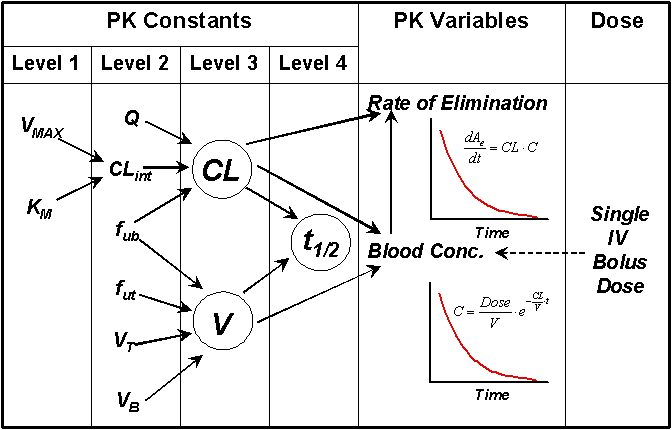
The arguments presented here are summarized in Figure 5 in terms of hierarchy of the major pharmacokinetic parameters (constants) and their interdependence. Furthermore, the effects of these kinetic parameters on the blood concentrations and elimination rate after a single intravenous dose are demonstrated.
Although the hypothetical drug used here only underwent hepatic metabolism, the principles discussed here are equally applicable for drugs undergoing renal and/or hepatic elimination. When different organ clearances are involved in the drug elimination, the total CL will be a summation of the individual clearances. This, however, does not change the dependency of the rate of elimination on total CL.