J Pharm Pharmaceut Sci (www.cspscanada.org) 9(2):262-269, 2006
In silico prediction of drug solubility in water-ethanol mixtures using Jouyban-Acree model
A. Jouyban, W.E. Acree Jr.
Faculty of Pharmacy and Drug Applied Research Center, Tabriz University of Medical Sciences, Tabriz, Iran; Department of Chemistry, University of North Texas, Denton, TX, USA
Received May 29, 2006; Revised June 21, 2006; Accepted July 24, 2006; Published, August 25, 2006.
Corresponding author: Dr. A. Jouyban, Faculty of Pharmacy and Drug Applied Research Center, Tabriz University of Medical Sciences, Tabriz Iran, Email: ajouyban@hotmail.com
ABSTRACT: PURPOSE: A predictive method was proposed to predict solubility of drugs in water-ethanol mixtures at various temperatures based on the Jouyban-Acree model. The model requires the experimental solubility data of the drug in mono-solvent systems. METHODS:The accuracy of the proposed prediction method was evaluated using collected experimental solubility data from the literature. The proposed method is:
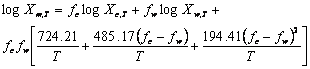
Where Xm,T, Xc,T and Xw,T are the solute solubility at temperature (T) in mixed solvent and neat cosolvent and water, respectively, fc and fw denote the solute free fraction of cosolvent (ethanol) and water. The average absolute error (AAE) of the experimental and the predicted solubilities was computed as an accuracy criterion and compared with that of a well-established log-linear model. RESULTS:The AAE (±SD) of the Jouyban-Acree and log-linear models were 0.19 (±0.13) and 0.48 (±0.28), respectively. The mean difference of AAEs was statistically significant (p<0.0005) revealing that the Jouyban-Acree model was provided more accurate predictions. Although the log-linear model was used to predict solubility at a fixed temperature (25 or 23 °C), the results also showed that the model could be employed to predict the solubility in solvent mixtures at various temperatures. CONCLUSION: More accurate predictions were provided using the Jouyban-Acree model in comparison with a previously established log-linear model of Yalkowsky. The prediction methods were successfully extended to predict the solubility in water-ethanol mixtures at various temperatures.
INTRODUCTION
Solubilization of a drug/drug candidate is still a challenging area in pharmaceutical industry. One of the most common procedures to increase poor solubility of a drug is the cosolvency method. The history of systematic solubility studies in water-cosolvent mixtures back to a couple of decades ago. Paruta and co-workers (1) have studied the solubility of different drugs in water-cosolvent mixture and tried to explain the solubility behavior using the dielectric constant of the mixed solvent (1). In 1972, Yalkowsky and co-workers (2) proposed the log-linear equation to represent the drug solubility in water-cosolvent mixtures using solute free volume fraction of the cosolvent. Martin and co-workers (3) have extended the Hildebrand solubility approach to describe solubility of polar/semi-polar drugs in aqueous mixtures of a model cosolvent, dioxane. The excess free energy approach (4), mixture response surface (5), the phenomenological model (6), the combined nearly ideal binary solvent/Redlich-Kister equation, the Jouyban-Acree model (7, 8), the modified Wilson model (9) and fluctuation theory (10) have also been employed to model drug solubility data in aqueous binary solvent mixtures. From these models the log-linear model is the most simplest model and the Jouyban-Acree model is the most accurate one (8).
In addition to the models mentioned above, a number of attempts have been made to build a general correlative/predictive equation for an aqueous-cosolvent mixture (11, 12) or a group of structurally related drugs in a given aqueous binary solvents (13, 14). Most of the models required relatively complex computational methods, a number of experimental data points to train the model, and also a knowledge of physico-chemical properties such as molar volume, solubility parameter etc of the solute and solvents.
The log-linear model has been preferred, because of its simplicity and applicability in pharmaceutical industry where researchers are more interested in models requiring simple and easy computational operations.
The aim of this work is to establish model constants of the Jouyban-Acree model to predict the solubility of various solutes in water-ethanol mixtures at different temperatures employing solubilities of the solute in water and ethanol. The accuracy of the proposed method is compared with that of the log-linear equation.
COMPUTATIONAL METHODS
The algebraic mixing rule (2) or log-linear model was expressed by:
![]() (1)
(1)
where Xm is the solute’s solubility in water-cosolvent mixtures, fc and fw the volume fractions of cosolvent and water in the absence of the solute, Xc and Xw the mole fraction solubilities in neat cosolvent and water, respectively. By replacing fw with (1-fc), equation 1 could be re-written as:
![]() (2)
(2)
![]() or
or
![]() (3)
(3)
In which ![]() is the solubilization power of a cosolvent. The
is the solubilization power of a cosolvent. The ![]() was correlated to the octanol-water partition coefficient (P) of the solute as (2):
was correlated to the octanol-water partition coefficient (P) of the solute as (2):
![]() (4)
(4)
the regression parameters S0 and S1 are specific for the solvent and independent of the solutes. The numerical values of S0 and S1 for 15 widely used cosolvents were reported (15). The S0 and S1 terms for water-ethanol solvent system collected from different references computed using equation 4 were listed in Table 1. Equations 3 and 4 could be combined as:
![]() (5)
(5)
Or
![]() (6)
(6)
S0 and S1 values were computed using a no intercept least square analysis in this work. The previously reported S0 and S1 values were computed by regressing slope of the log-linear model against logP of the solutes.
Table 1. Numerical values of intercept and slope of linear relationship of the solubilization power of the cosolvent and logarithm of partition coefficient of the solute (i.e., S0 and S1) collected from different works and the average absolute error (AAE) values.
No. |
S0 |
S1 |
Reference for the constant |
AAE (±SD) at 25 °C |
AAE (±SD) at various temperatures |
1 |
0.402 |
0.903 |
22 |
0.51 (±0.29) |
0.47 (±0.27) |
2 |
0.30 |
0.95 |
15 |
0.53 (±0.29) |
0.48 (±0.28) |
3 |
0.40 |
0.93 |
11 |
0.51 (±0.29) |
0.46 (±0.28) |
4 |
0.309 |
0.945 |
This work |
0.53 (±0.29) |
0.48 (±0.28) |
The log-linear model presents ideal mixing behaviour of the solutions and could be extended to the models possessing more constants representing the non-ideality of the observed solubility data. As it has been shown in a previous paper (8), employing more model constants (curve-fitting parameters) provide more accurate correlation and obviously more accurate prediction. The Jouyban-Acree model is one of these models which provided the most accurate correlation among similar cosolvency models (8). In addition to solubility data, it was used to calculate other pharmaceutically important physico-chemical properties in mixed solvent systems that briefly reviewed in a recent paper (16). Its basic form for calculating a solute solubility in a water-cosolvent mixture is:
![]() (7)
(7)
where Ai the solvent-solvent and solute-solvent interaction terms (17) computed using a no-intercept least square analysis (18). The Ai coefficients in equation 7 do have theoretical significance in that each coefficient is a function of two-body and three-body interaction energies that describe the attractions between the various molecules in solution (17). In the case of a solute dissolved in water-cosolvent mixtures, the basic thermodynamic model from which equation 7 was derived included all six possible two-body (c-c, w-w, s-s, c-w, c-s and w-s) and all ten possible three-body (c-c-c, w-w-w, s-s-s, c-c-w, c-w-w, c-c-s, c-s-s, w-w-s, w-s-s and c-w-s) molecular interactions between water (w), cosolvent (c) and solute (s) molecules. Equation 7 was derived by differentiating the integral excess Gibbs energy of mixing equation for the mixture containing components w, c and s, expressed in terms of the 16 fore-mentioned two-body and three-body interaction energies, with respect to the number of moles of solute. Raoult’s law was used for the entropic contribution in the integral Gibbs energy of mixing equation. More details of the derivation of the model could be found in a previous paper (17). In the derivation of equation 7, it is written in terms of logarithms of the mole fraction solubilities of the solute, rather than as 2.303RTlogXm in which R is the gas constant and T is the absolute temperature. The 2.303RT is incorporated into the Ai terms and it is possible to re-write the model to calculate the solubility of drugs in binary solvents at various temperatures (19) as:
![]() (8)
(8)
where Xm,T, Xc,T and Xw,T are the solubility of the solute in solvent mixture, cosolvent and water in the absence of the solute at temperature (T, K) and Ji is the model constant. By this extension, one is able to predict solubilities in mixed solvents at various temperatures which quite beneficial to pharmaceutical industry.
The average absolute error (AAE) was used to check the accuracy of the prediction method and is calculated using equation 9.
![]() (9)
(9)
in which N is the number of solubility data points.
RESULTS
Available experimental mole fraction solubility data of drugs in water-ethanol mixtures at a constant and various temperatures were collected from the literature. The data sets containing Xc and Xw values were included in this study since the Jouyban-Acree model requires these values as input data. Details of data, AAE values, overall AAE (± SD) and also the references were listed in Table 2. The data (at fixed and various temperatures) was fitted to equations 6 and 8, and the trained models were:
![]() (10)
(10)
and
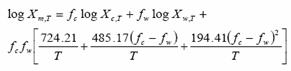 (11)
(11)
The minimum AAE for equation 10 was 0.18 (for norleucine) and the maximum value was 1.36 (for sulphamethiazine) and the overall AAE (± SD) was 0.48 (±0.28). The reported S0 and S1 values listed in Table 1 were used to predict the solubility of solutes in water-ethanol mixtures and the overall AAEs (± SD) were also listed in Table 1. There are no significant differences between AAE values for different sets of S0 and S1 values. This means that the differences in numerical values of S0 and S1 have no significant effect on the prediction capability of the log-linear model. The model was established to compute solubility data at 25 °C, however, it was used to predict solubility at 23 °C (20).
There is no independent variable representing the effect of temperature on the solubility of a solute in water-ethanol mixture except logXw which should be used at the same temperature of interest. A further numerical analysis is carried out at 25 °C and there is no significant difference between AAE of the log-linear model at 25 °C and various temperatures (see the corresponding AAE reported in Table 2 for set numbers 18 and 20).
To obtain the most accurate predictions, one should also use logP at the temperature of interest. Figure 1 showed the observed versus predicted solubilities using equation 10.
Table 2. Details of solubility data in water-ethanol mixtures, number of data points (N), temperature (t) and average absolute error (AAE) for equations 10 and 11
| No | Solute |
Ref |
t |
At various temperatures |
At 25 °C |
||||
|
|
|
|
N |
Eq 11 |
Eq 10 |
N |
Eq 11 |
Eq10 |
1 |
Acetanilide |
26 |
25 |
13 |
0.14 |
0.61 |
13 |
0.14 |
0.61 |
2 |
Alanine (Beta) |
27 |
25 |
7 |
0.40 |
0.57 |
7 |
0.40 |
0.57 |
3 |
Alanine (DL) |
27 |
25 |
7 |
0.14 |
0.38 |
7 |
0.14 |
0.38 |
4 |
Aminocaproic acid (e) |
27 |
25 |
7 |
0.52 |
0.73 |
7 |
0.52 |
0.73 |
5 |
Asparagine (L) |
27 |
25 |
5 |
0.12 |
0.39 |
5 |
0.12 |
0.39 |
6 |
Aspartic acid (L) |
27 |
25 |
7 |
0.16 |
0.25 |
7 |
0.16 |
0.25 |
7 |
Benzo [a] pyrene |
22 |
23 |
6 |
0.15 |
0.32 |
- |
- |
- |
8 |
Caffeine |
20 |
25 |
11 |
0.15 |
0.42 |
11 |
0.15 |
0.42 |
9 |
Chrysene |
22 |
23 |
6 |
0.09 |
0.33 |
- |
- |
- |
10 |
Furosemide |
28 |
25 |
13 |
0.30 |
0.38 |
13 |
0.30 |
0.38 |
11 |
Glycine |
27 |
25 |
7 |
0.19 |
0.35 |
7 |
0.19 |
0.35 |
12 |
Glycylglycine |
27 |
25 |
7 |
0.29 |
0.48 |
7 |
0.29 |
0.48 |
13 |
Hexachlorobenzene |
22 |
23 |
6 |
0.26 |
0.21 |
- |
- |
- |
14 |
Leucine (L) |
27 |
25 |
7 |
0.09 |
0.19 |
7 |
0.09 |
0.19 |
15 |
Nalidixic acid |
29 |
25 |
13 |
0.08 |
0.46 |
13 |
0.08 |
0.46 |
16 |
Niflumic acid |
20 |
25 |
9 |
0.52 |
0.66 |
9 |
0.52 |
0.66 |
17 |
Norleucine (DL) |
27 |
25 |
7 |
0.10 |
0.18 |
7 |
0.10 |
0.18 |
18 |
Oxolinic acid |
21 |
20-40 |
55 |
0.12 |
0.42 |
11 |
0.11 |
0.40 |
19 |
Paracetamol |
30 |
25 |
13 |
0.09 |
0.69 |
13 |
0.09 |
0.69 |
20 |
Paracetamol |
31 |
20-40 |
35 |
0.16 |
0.88 |
7 |
0.15 |
0.90 |
21 |
Pentachlorobenzene |
22 |
23 |
6 |
0.27 |
0.24 |
- |
- |
- |
22 |
Perylene |
22 |
23 |
6 |
0.09 |
0.29 |
- |
- |
- |
23 |
Salicylic acid |
25 |
25 |
11 |
0.15 |
0.39 |
11 |
0.15 |
0.39 |
24 |
Sulphamethiazine |
32 |
25 |
11 |
0.25 |
1.36 |
11 |
0.25 |
1.36 |
25 |
Sulphanilamide |
32 |
25 |
12 |
0.06 |
1.04 |
12 |
0.06 |
1.04 |
26 |
Valine (DL) |
27 |
25 |
7 |
0.06 |
0.28 |
7 |
0.06 |
0.28 |
|
Mean+/-SD |
|
|
|
0.19 ± 0.13 |
0.48 ± 0.28 |
|
0.19 ± 0.14 |
0.53 ± 0.29 |
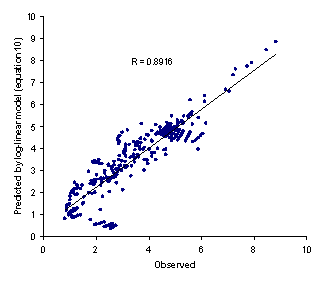
Figure 1. Observed logXm versus predicted values using equation 10
In using the proposed prediction method, one should consider that:
1. Solubility of the solute of interest in water and ethanol should be determined experimentally and used as input variables of the model.
2. All predicted solubility units were the same as solubility unit of Xc,T and Xw,T used in the model (i.e., using Xc,T and Xw,T expressed as mole fraction, the predicted solubilities were in mole fraction unit, using Xc,T and Xw,T expressed as mole/L, the predicted solubilities were in mole/L etc.).
3. To provide more accurate predictions, the solvent composition of the mixed solvent system should be expressed as volume fraction (fc for volume fraction of ethanol and fw for volume fraction of water).
4. Temperature should be expressed as absolute temperature (K).
The minimum AAE for equation 11 was 0.06 (for valine) and the maximum value was 0.52 (for aminocaproic acid) and the overall AAE (± SD) was 0.19 (±0.13). There was significant difference between AAE of equations 10 and 11 (paired t-test, p<0.0005) revealing that the proposed method is capable of providing more accurate predictions when compared with the log-linear model. Figure 2 showed the observed versus predicted solubilities using equation 11. In addition to less AAE value, the higher correlation coefficient of equation 11 (R=0.9871) in comparison with that of equation 10 (R=0.8916) indicate the superiority of the proposed model to the log-linear model.
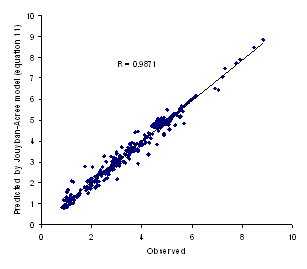
Figure 2. Observed logXm versus predicted values using equation 11
DISCUSSION
The importance of aqueous solubility of drugs can be recognized at all steps of drug discovery and development. The solubility determines absorption, distribution and elimination of a drug. The most commonly used solubilization technique is the cosolvency and any in silico solubility prediction method can contribute significantly to the reduction of the overall cost and also speed up the drug development process. The simplest available method is the log-linear model which is applicable for solubility profiles showing no solubility maximum in mixed solvents. This is not the case for most of the solubility profiles in water-pharmaceutically interested cosolvent mixtures and there is a number of solubility profiles, such as solubility of some drugs in water-ethanol mixtures (as examples see references 20, 21), which show solubility maximum. As previously reported (22), a couple of reasons could be provided to explain these deviations from log-linear relationship. As shown in this work, the log-linear model produces relatively high error and this could be considered as another limitation to the model. In order to estimate the solubility of different solutes in a given binary solvent systems using the log-linear model, Millard et al. (11) reported the solubilization power of four common pharmaceutical cosolvents. From this correlation, each cosolvent has two constant values that were reported (11) and using this method, the aqueous solubility of a drug and its partition coefficient are required as input data to predict the solubility in water-cosolvent mixtures. Machatha and Yalkowsky (23) used half slope of the log-linear solubilization power (![]() ) to predict the cosolvent fraction giving the maximum solubility of a drug. The required data were partition coefficient of the cosolvent and the solute. The partition coefficient (logP) of a solute could be determined experimentally or calculated using software like ClogP®, ACDlogP and KowWin® and the logP data calculated using ClogP® software provided more accurate results (24). This prediction could help pharmaceutical industry to speed up the optimization of liquid drug formulations where the cosolvent fraction should be kept as low as possible, usually less than 0.5. Rytting et al. (12) proposed quantitative structure-property relationships (QSPRs) to compute solubility of drug/drug like molecules in water-PEG 400 mixtures using molecular descriptors computed by Cerius software and different sets of model constants for each binary solvent composition. They tested the applicability of the QSPRs using solubility of 122 drugs determined at 23 °C and did not check possible hydrate/solvate formation in the solutions where a number of solutes possess solvates/polymorphic forms and this point should be considered in the future works. Prediction of solubility of different solutes in various solvent systems with an acceptable error range is the ultimate goal of predictions in this area. The produced prediction errors for such models are relatively high and as a result the models cannot be recommended for pharmaceutical industry. An accurate predictive model was not proposed so far. However, considering rapid growth in databases and also computational methods, it is expected that better predictive methods will be presented in the near future. As shown in our earlier works (8, 19, 25), the Jouyban-Acree model provides accurate solubility predictions for water-cosolvent mixtures at various temperatures. The main drawback of the model is its constants which should be trained using a limited number of experimental solubility data. The proposed model in this work which is trained using solubility data in water-ethanol mixtures is able to reproduce solubility profile of a drug/drug candidate at various temperatures using solubility data in neat water and ethanol and the AAEs are within acceptable error range when it is compared with the log-linear model. It is obvious that the improvement of the prediction methods should be continued until achievement of the prediction error comparable to experimental relative standard deviations.
) to predict the cosolvent fraction giving the maximum solubility of a drug. The required data were partition coefficient of the cosolvent and the solute. The partition coefficient (logP) of a solute could be determined experimentally or calculated using software like ClogP®, ACDlogP and KowWin® and the logP data calculated using ClogP® software provided more accurate results (24). This prediction could help pharmaceutical industry to speed up the optimization of liquid drug formulations where the cosolvent fraction should be kept as low as possible, usually less than 0.5. Rytting et al. (12) proposed quantitative structure-property relationships (QSPRs) to compute solubility of drug/drug like molecules in water-PEG 400 mixtures using molecular descriptors computed by Cerius software and different sets of model constants for each binary solvent composition. They tested the applicability of the QSPRs using solubility of 122 drugs determined at 23 °C and did not check possible hydrate/solvate formation in the solutions where a number of solutes possess solvates/polymorphic forms and this point should be considered in the future works. Prediction of solubility of different solutes in various solvent systems with an acceptable error range is the ultimate goal of predictions in this area. The produced prediction errors for such models are relatively high and as a result the models cannot be recommended for pharmaceutical industry. An accurate predictive model was not proposed so far. However, considering rapid growth in databases and also computational methods, it is expected that better predictive methods will be presented in the near future. As shown in our earlier works (8, 19, 25), the Jouyban-Acree model provides accurate solubility predictions for water-cosolvent mixtures at various temperatures. The main drawback of the model is its constants which should be trained using a limited number of experimental solubility data. The proposed model in this work which is trained using solubility data in water-ethanol mixtures is able to reproduce solubility profile of a drug/drug candidate at various temperatures using solubility data in neat water and ethanol and the AAEs are within acceptable error range when it is compared with the log-linear model. It is obvious that the improvement of the prediction methods should be continued until achievement of the prediction error comparable to experimental relative standard deviations.
CONCLUSION
In conclusion, the proposed model showed more accurate predictions in comparison with a previously established log-linear model. The prediction methods were successfully extended to the various temperatures which is obviously required in pharmaceutical area in drug formulation and also crystallization studies.