J Pharm Pharmaceut Sci (www.cspscanada.org) 9(2):238-244, 2006
A common profile for polymer-based controlled releases and its logical interpretation to general release process
Songjun Li, Yan Shen, Wuke Li, Xiao Hao
Key Laboratory of Pesticide & Chemical Biology of Ministry of Education, College of Chemistry, Central China Normal University, Wuhan, China
Received March 19 2006; Revised, July 25, 2006, Accepted, July 26, 2006, Published July 27 2006
Corresponding author: Dr. Songjun Li, Central China Normal University College of Chemistry, China, E-mail: Lsjchem@msn.com
ABSTRACT: Purpose. The release of drug from a polymeric matrix is complicated. It often involves drug diffusion, interface movement and various interactions. It also shows a dependence on the length of polymer rod. With Lc as the ‘critical length’, three different phases can be distinguished from the kinetic process. Prior to reaching Lc, the interface movement plays a key role on determining the release. Otherwise, the drug diffusion can dominate the release process. Near Lc, however, both factors are involved. The rate of interface movement is closely associated with the time and position in the polymer rod. Taking these characters into account, a common model is presented in this article to be tentatively used to interpret the release process. These results provide preliminarily an insight into the understanding of controlled release process.
INTRODUCTION
Several models are available for interpretation of controlled releases behavior [1-4]. For example, Higuchi’s square-root equation is a classical model that assumes drug diffusion for the release from a polymeric matrix (insoluble in the solvent). As Higuchi recognized, the extraction of drug from the matrix could result in a sharp interface. In the section between the interface and the solvent, the drug was leached out. However, nothing was extracted behind the interface. As he also recognized, the concentration downstream of the interface was usually less than the concentration upstream of the interface and this gradient was determined chiefly by the rate that drug diffuses away from the interface into a perfect sink. When dealing with this profile, Higuchi made an approximation that this gradient was linear and was in a ‘pseudo steady-state’. Subsequently, Fick’s first law was applied across the interface for the determination of the movement rate. Henceforward, based on various boundary conditions, several models have been proposed. In this aspect, the following three equations hold the special position and are currently in common use due to their simplicity and applicability:
Higuchi’s square-root Eqn:
![]() (1)
(1)
Zero-order model Eqn:
![]() (2)
(2)
Ritger-Peppas’ empirical Eqn:
![]() (1/2<n<1) (3)
(1/2<n<1) (3)
Here M t and M ∞ are respectively the accumulative and the maximal amounts of drug released, t, the time, k as well as n are constants. It has been well known that Equations (Eqns) 1, 2 and 3 describe respectively the release processes under the controls of drug diffusion (Fickian or Case I mechanism), interface movement (Case II mechanism) and anomalous release with respect to the applicability. In the case of Fickian mechanism, the rate of drug diffusion is much less than that of polymer relaxation. Thus the release will be determined chiefly by the drug diffusion in such a system. Because of this, a large concentration gradient in both sides of the interface may be observed. For Case II system, the reverse is true. The rate of drug diffusion is much larger than that of polymer relaxation. A characteristic of Case II mechanism is that the rate of interface movement is constant, so that the amount released is proportional directly to time.
In the anomalous case, the rates of drug diffusion and polymer relaxation are about in the same size. Therefore the observable result is usually a combine contribution of both factors. In the present opinion [5], Fickian and Case II mechanisms can be regarded as two limiting boundaries with the anomalous release in between. As noted, these Eqns can be unified into a common expression though differing from the exponent:
![]() (4)
(4)
On some occasions, it has also been found that the exponent could be less than 1/2 [6,7]. This reveals that there are some common-grounds existing between various controlled release mechanisms. A typical feature from various controlled releases is that the extraction of drug from the polymeric matrix is a result of solvent penetration. Likewise, despite the specific process, the total amount of drug containing in the polymer and the solvent is a fixed value. Hence, one may consider a common profile for various controlled releases patterns.
Micromechanism analysis of polymer-based controlled releases
Fig.1 presents a general scheme of polymer-based controlled releases [8,9]. A rod or sheet, made of a polymer matrix and drug, is placed in contact with a solvent. As the interface advances, the drug suspended in the matrix will be released and diffused away into the solvent. Originally, the concentration downstream of the interface (in the rubbery polymer) is lower than that upstream of the interface (in the glassy polymer) and that a sharp break exists in both sides. Progressively with time, the interface moves further toward the unpermeated matrix. Hence, the path for drug diffusion from the interface to the sink gets correspondingly longer. This results in a gradual accumulation for drug in the rubbery polymer and an increased concentration downstream of the interface. Eventually, when the path for drug diffusion reaches a ‘critical length’ (Lc) [9], the concentration downstream of the interface will become equal to that upstream of the interface. Beyond the critical point, the moving front will not affect the concentration profile due to the relative slower rate for the drug diffusion.
Basing on this general model, three distinguished phases (nominated as A, B and C; Fig.2) with difference in the release behavior can be assumed. In phase A, the path for drug diffusion is much shorter than Lc. The succeeding process is phase B which has a length near Lc, followed by the phase C. In phase A, the drug released from the interface can diffuse away easily due to the short path, in relation to the slow interface movement. As a result, the release is controlled chiefly by the interface movement in this phase. For the phase C, on the other hand, the reverse is true. This process is the classic ‘drug diffusion in a rod with known initial and boundary conditions’ [10,11]. In the phase B, near the critical length, the release is considerably complicated and involves the combine contribution of both factors. Therein, the concentration downstream of the interface is close to the one upstream of the interface, so an anomalous release or no release would be observed. Now, with this in hand, one can comprehend well three mentioned models.

Figure 1. Schematic presentation of polymer-based controlled releases
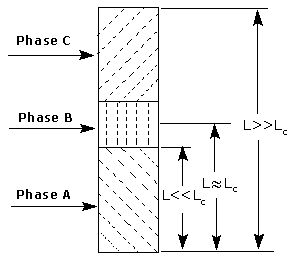
Figure 2. Micromechanism of controlled releases
Energy change of polymer-based controlled releases
As already discussed, polymer-based controlled releases are actually complicated and often involve drug diffusion, interface movement and various interactions. As the interface advances upward (Fig.3), the embedded drug is released and diffuses away into the sink. In the meanwhile, the permeated polymer is converted into the rubbery polymer due to the swelling of solvent. Clearly, the interactions involved by releases include mainly solvent-glassy polymer (ESG; J/cm3), solvent-rubbery polymer (ESR; J/cm3), drug-glassy polymer (ε DG; J/g) and drug-rubbery polymer (ε DR; J/g).
The change of energy, however, includes the transition of polymer (QGR; J/cm3) and drug dissolution (HD; J/g). Now, considering the change of energy (![]() ) along the microunit passed by the interface, one can normally show:
) along the microunit passed by the interface, one can normally show:
![]() (5)
(5)
Here, C 0 is the concentration of drug embedded in the glassy polymer (g/cm3) and the minus ‘-’ indicates the opposite orientation regarding the diffusion of drug and the permeation of solvent. In the right of the Eqn, the first and the second items summarize the changes of energy induced by the solvent permeation and drug diffusion. The latter two present, however, the changes of energy because of the transition of polymer (from a glassy state into a rubbery body) and the dissolution of drug. Integrating Eqn (5) from ![]() to
to ![]() will give:
will give:
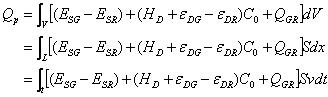 (6)
(6)
Here S is the cross-section area of matrix, x, the distance passed, t, the time, and v is the rate of interface movement.
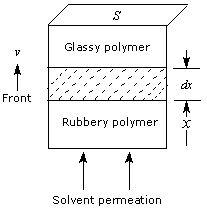
Figure 3. Schematic presentation of the moving interface
Rate of interface movement
As already explained, the advance of solvent can involve various interactions. Also the earlier passed polymer can hinder the latter permeation of solvent. Hence, the rate of interface movement, as well as the activation energy, is not a constant but is actually a function of time and position in most cases [14,15]:
![]() (7)
(7)
Here v0 is the rate of front movement at the instant that the matrix contacts with the solvent, and v is the rate at ![]() and
and![]() . Now, taking the effect of time on the activation energy into account, one can show in a fixed x:
. Now, taking the effect of time on the activation energy into account, one can show in a fixed x:
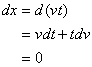 (8)
(8)
Correlating Eqn (8) with (7) can present:
![]() (9)
(9)
This thus gives:
![]() (10)
(10)
Similarly, one can show the effect of position in a fixed t:
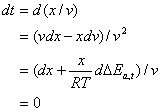 (11)
(11)
This therefore presents:
![]() (12)
(12)
Here a and b are the integral constants. Now, according to mathematical theory, ![]() can be sought into such a form:
can be sought into such a form:
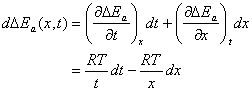 (13)
(13)
Clearly, the change of activation energy with time and position is:
![]() (14)
(14)
Here c is also an integral constant. Substituting Eqn (14) into (7) can show:
![]() (15)
(15)
Now, combining Eqn (15) with (6) will give:
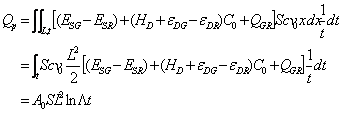 (16)
(16)
Here, A0 is an interaction constant (coming from the unification of various energy constants), L, the length of polymer rod passed by the interface at t=t, and ![]() is an integral constant (related to the position of interface at t=t).
is an integral constant (related to the position of interface at t=t).
Thermodynamic analysis of in vitro release
Change of chemical potential, one can learn some inherent information involved in the process. According to thermodynamic theory, the basic expression of chemical potential is:
![]() (17)
(17)
Here,![]() and
and![]() are the actual and the standard chemical-potentials of specific component, C and
are the actual and the standard chemical-potentials of specific component, C and![]() , the corresponding concentrations. As already stated, the advance of interface will result in a release from the front. This, in time, makes a change of relative concentration in both sides of the interface, thereby bringing an effect on the chemical potential. At the concentration upstream of the interface, the chemical potential of drug is:
, the corresponding concentrations. As already stated, the advance of interface will result in a release from the front. This, in time, makes a change of relative concentration in both sides of the interface, thereby bringing an effect on the chemical potential. At the concentration upstream of the interface, the chemical potential of drug is:
![]() (18)
(18)
The corresponding chemical potential in the concentration downstream, however, is:
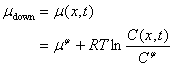 (19)
(19)
The change of chemical potential in the both sides of interface thus is:
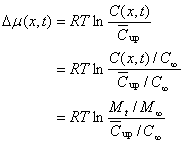 (20)
(20)
Where, M t and M ∞ are the same as that in Eqns (1), (2) and (3), presenting the accumulative and the maximal amounts of drug released.![]() and
and![]() are the average and the maximal concentrations in both sides of the interface. Now, according to thermodynamic theory, one can show:
are the average and the maximal concentrations in both sides of the interface. Now, according to thermodynamic theory, one can show:
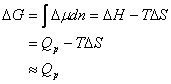 (21)
(21)
The Eqn obtained is due to the limited change in the movement state of particles between the glassy and the rubbery polymers. Integrating Eqn (21) will present:
 (22)
(22)
Combining Eqns (21) and (22) with (16) can give:
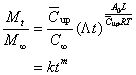 (23)
(23)
Clearly, Eqn (23) is exactly the expression of Eqn (4). The exponent m is relied apparently on various interactions and the length of polymer rod. Now, with this background in hand, one can comprehend why some reported releases with similar operations exhibited different results. Also it is not difficult to see why several models have been proposed for various release processes.
Interpretation to common process
Fig.4 presents a typical profile of releasing BB (brilliant blue FCF) from silica-PNIPAAm [poly (N-isopropylacrylamide)] gel (carried out by Suzuki et al) [16]. As observed, there is initially a rapid increase in the released amount and then a slow approach to 100%. Based on the previous elucidation, the rapid release in the beginning is normally expected to be a Case II-typed release and the slower approach to the limitation of 100% is, however, the Fickian process. Apparently, according to any one from Eqns (1), (2) and (3), it is difficult in common sense to comprehend such a process that involves sometimes Case II-typed release and sometimes Fickian mechanism under a specific condition. Similarly, for the release of testosterone from poly (ethylene oxide) matrix (Fig.5), an exponent less than 1/2 (n=0.394) can be obtained [17]. In literature, quite some analogous example is also available [18-20]. Clearly, if regarding Fickian and Case II mechanisms as the limiting boundaries, one would not anticipate appearance of such behaviors. Now, with Eqn (23) in hand, one can easily know the probable cause. The controlled release is usually more complicated than some simplified models, which can involve various interactions among solvent, drug and polymer. Also the process is intrinsically related to the length of polymer. Prior to reaching the Lc, the interface movement, the slow step, can play an important role on affecting the process. As a result, a Case II-typed release is observed. Near the Lc, the release observed is a combine contribution of the interface movement and drug diffusion. Otherwise, the slow step at the drug diffusion will dominate the release process.
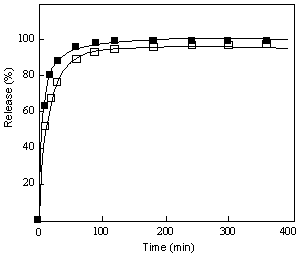
Figure 4. Release of BB from the silica-PNIPAAm gel
CONCLUSION
The mechanism of controlled release has attracted much attention. Presently, there are several models explaining the patterns of the release.
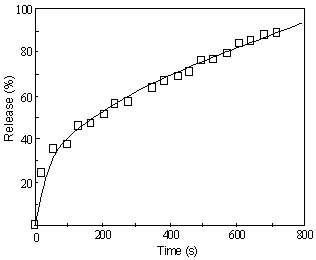
Figure 5. Release of testosterone from poly(ethylene oxide) matrix
Among them, Higuchi’s square-root Eqn, zero-order model and Ritger-Peppas’ empirical relationship held the special position because of the simple form and usability. As noted, these models can be unified into the same form though differing from the exponent. This indicates that there is considerable common-ground existing in various release processes. We have made an attempt to prove this point. As shown, the release of the drug from the polymeric matrix appears to be considerably complicated and can involve drug diffusion, interface movement and various interactions. The result indicates a dependency on the length of polymer rod. With Lc as the ‘critical length’, three phases with difference in the release behavior can be distinguished from the kinetic process. Prior to reaching Lc, the interface movement can play a key role in determining the release. Otherwise, the drug diffusion would dominate the release process. Near Lc, however, both factors are involved. Further, the rate of interface movement is closely related to the time and position in the polymer rod. Taking these characters into account, a unified model is presented in this article. It is also necessary to point out that these results are preliminary and that further work is necessary with respect to a clearer understanding.