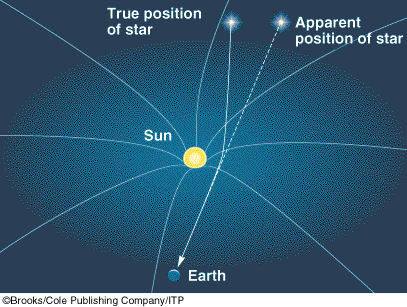
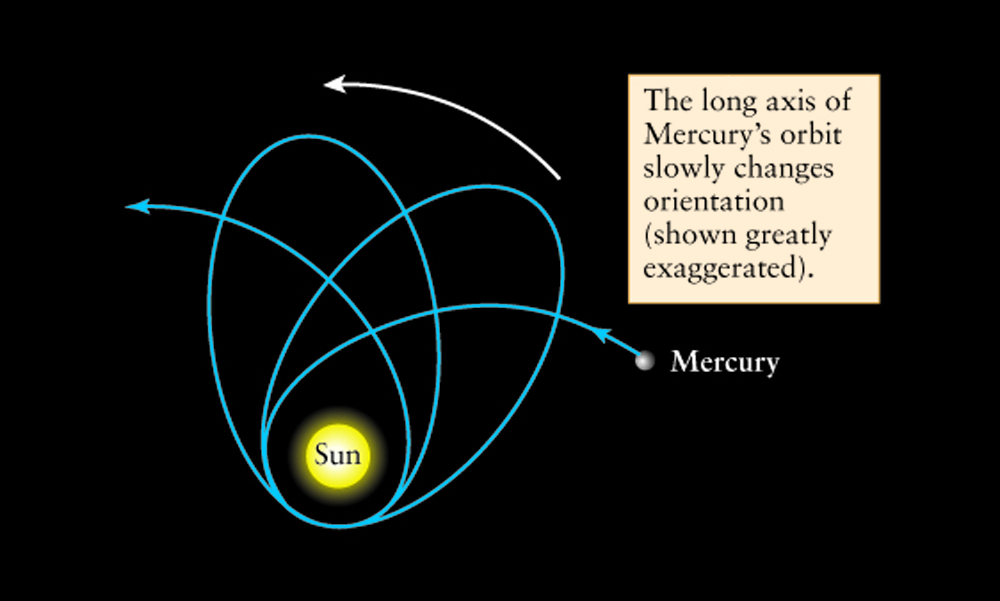
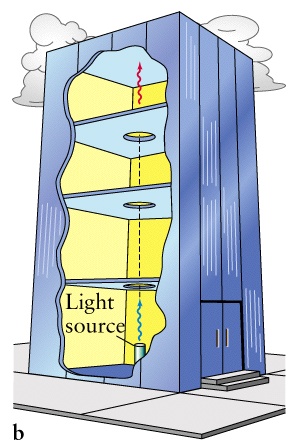
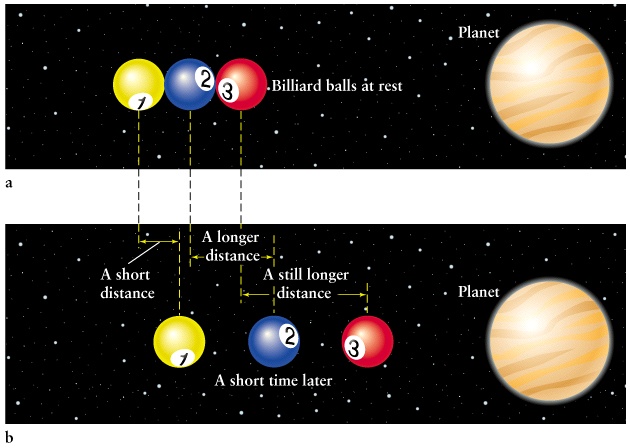
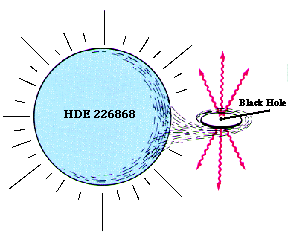
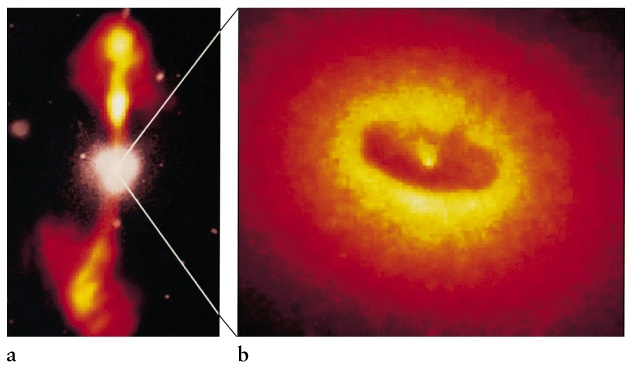
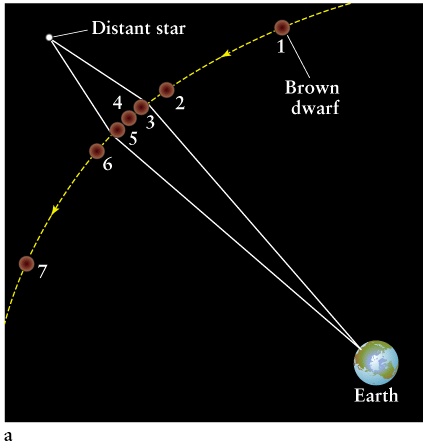
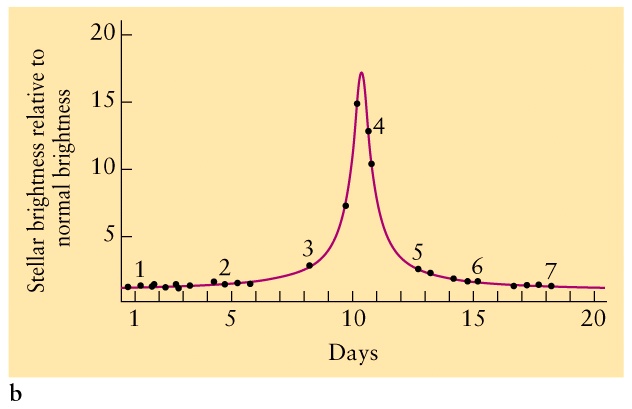
Black holes are simple!
- Although a star is approximately a sphere, it also has many
bumps (ie. prominences, flares, etc).
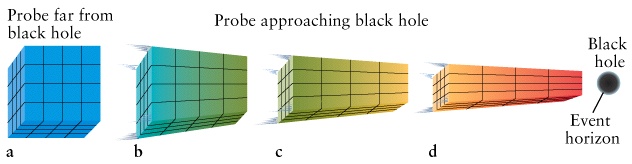
- As the density of a star increases, the size of bumps has to
decrease, ie. gravity smooths out bumps.
- For instance, mountains on a neutron star can't be much
higher than a centimetre.
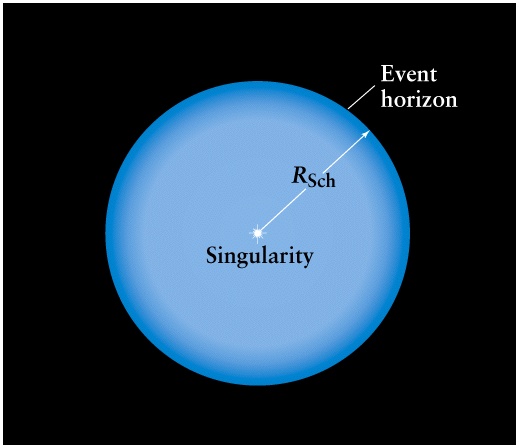
- In 1967, Werner Israel, (professor at the U of A, now retired in Victoria)
proved the "No Hair" Theorem which states that the event horizon
has to be perfectly smooth.
- From Israel's theorem, a black hole's properties are given
by just three numbers &minus mass M, electric charge Q and angular momentum L.
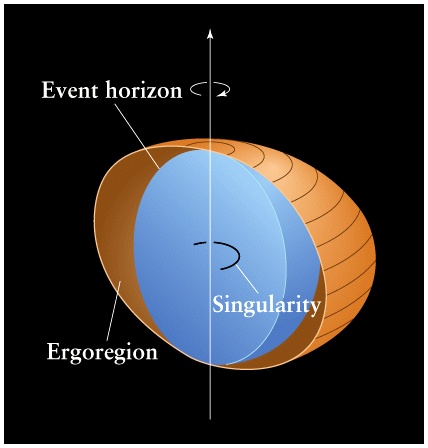
- If the black hole doesn't rotate, it must be exactly
spherical.
- If the black hole rotates, it must have a special ellipsoidal shape.
|
 |