- Oscillation appear when there is a restoring force that
acts on the system when it is out of equilibrium trying to bring it
back to equilibrium
- Consider spring with mass attached, which motion is governed by
the Hooke's law m a = F = - k x
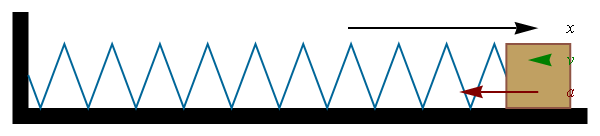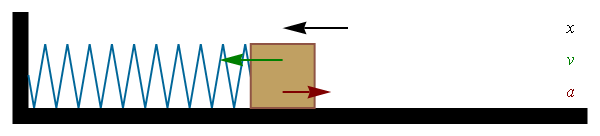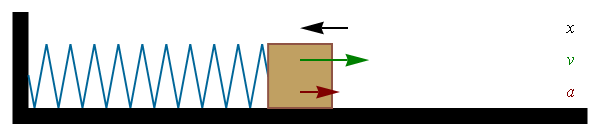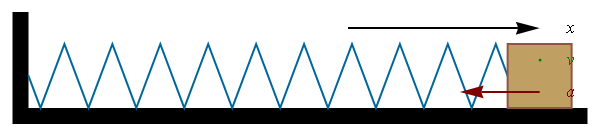
- How does the mass on the spring moves under Hooke's law ?
- One can solve differential equation
d2 x / d t2 = -(k/m) x , but one can just notice
that acceleration is proprtional and opposite to displacement
a = -(k/m) x exactly as it was for SHM !
- Thus, the mass on the spring experiences SHM
x = A cos(ω t + φ0) with
ω = (k/m)1/2
- "Initial phase" φ0 depends on what we chose as zero time
Oscillator that follows SHM is called Harmonic Oscillator
|